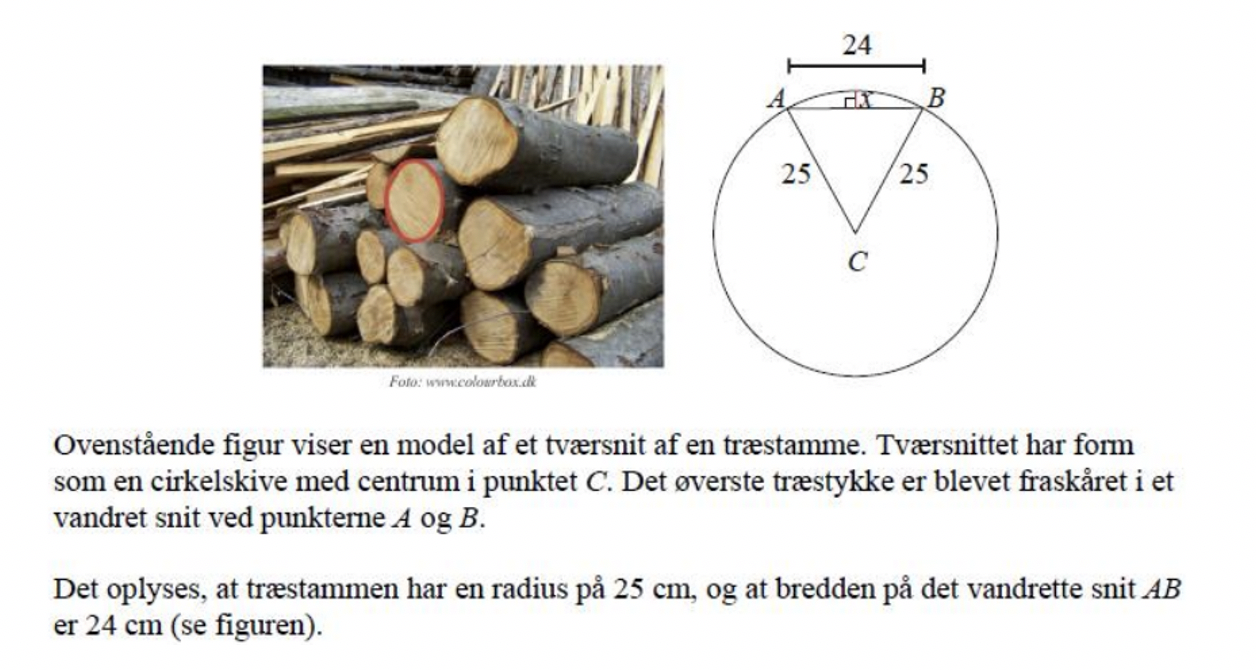
Matematik

cirkel

17. september 2020 af HTXS - Niveau: B-niveau

er blevet i tvivl, om hvordan denne opgave skal løses.

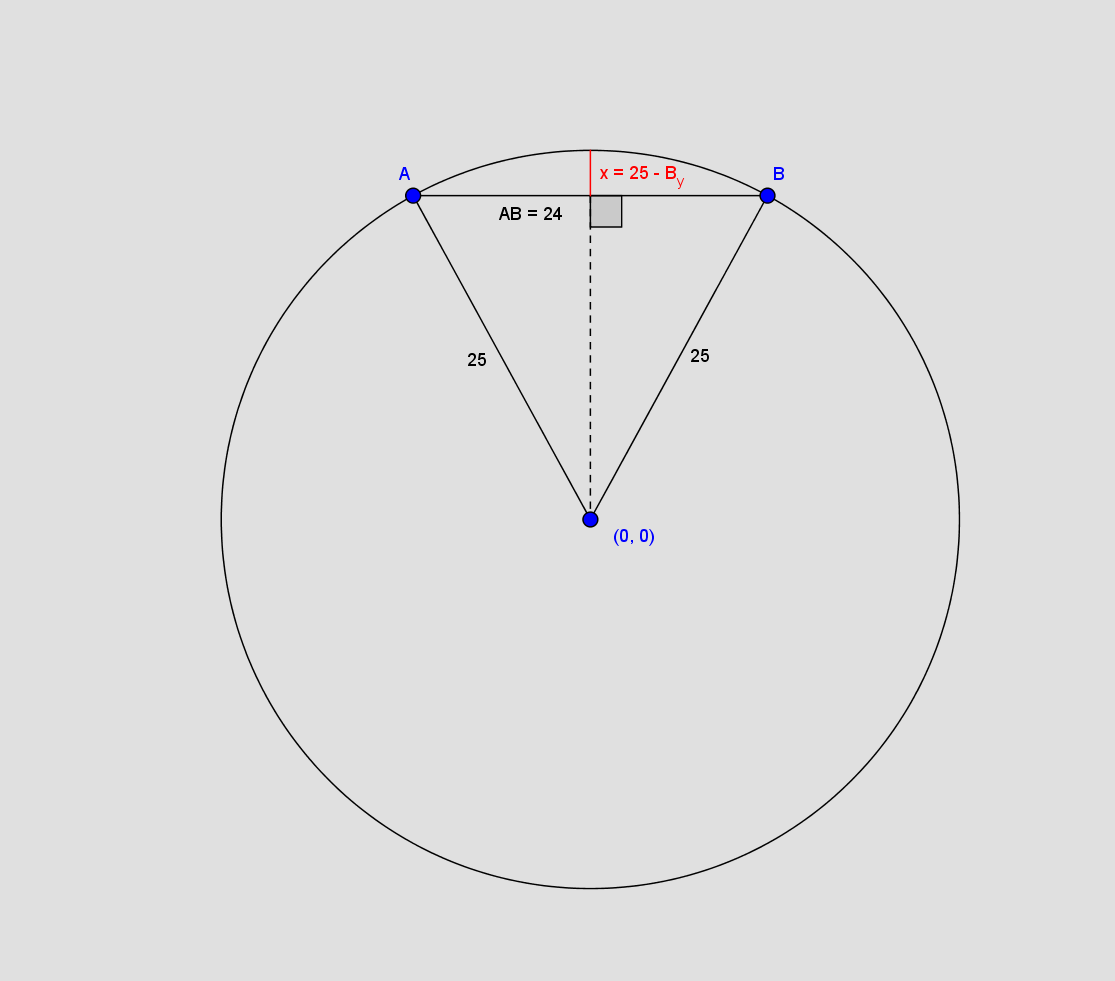
a) indlæg cirklen i et koordinatsystem, hvor punktet c ligger i (0,0)

dette har jeg gjort

b) bestem en ligning for cirklen i modellen

c) bestem koordinatsættet for punktet b, og bestem højden x af det fraskårne træstykke

jeg har vedhæftet figuren, jeg er ikke sikker på hvordan jeg løser b og c

Vedhæftet fil: Skærmbillede 2020-09-17 kl. 22.10.55.png

Brugbart svar (0)

Svar #1
17. september 2020 af ringstedLC

b) Find cirklens ligning i FS og indsæt det kendte.

c) B bestemmes med Pythagoras ved at nedfælde den vinkelrette på AB gennem C.

Brugbart svar (0)

Svar #2
18. september 2020 af PeterValberg

b) En ligning for cirklen kan bestemmes vha.

$(x-x_0)^2+(y-y_0)^2=r^2$

hvor (x₀, y₀) er cirklens centrum
r er cirklens radius

$(x-0)^2+(y-0)^2=25^2$

reducér udtrykket

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #3
18. september 2020 af mathon

$\small \begin{array}{llllll} \textup{beregning af }x\textup{:}\\& \begin{array}{llllll} (25-x)^2+12^2=25^2\quad \wedge\quad 0<x<25 \end{array} \end{array}$

Brugbart svar (0)

Svar #4
20. september 2020 af andre243g

Tak, forstår dog ikke helt, hvordan koordinatsættet for B skal udregnes

Brugbart svar (0)

Svar #5
20. september 2020 af andre243g

#3
$\small \begin{array}{llllll} \textup{beregning af }x\textup{:}\\& \begin{array}{llllll} (25-x)^2+12^2=25^2\quad \wedge\quad 0<x<25 \end{array} \end{array}$

Og er det muligt med en forklaring, om hvordan du har gjort dette? :D Beklager, jeg ikke lige forstår det helt

Brugbart svar (0)

Svar #6
20. september 2020 af andre243g

#4
Tak, forstår dog ikke helt, hvordan koordinatsættet for B skal udregnes

Har fundet ud af udregningen af koordinatsættet til B

Brugbart svar (0)

Svar #7
20. september 2020 af ringstedLC

#4: B_x = |AB| / 2, da linjestykket er parallelt med x-aksen. Indsæt B_x i cirklens ligning, da B opfylder denne:

$\begin{align*} {B_x}^2+{B_y}^2 &= 25^2\;,\;B_y>0 \\ B_y &=\;? \end{align*}$

Vedhæftet fil:__0.png

Brugbart svar (0)

Svar #8
20. september 2020 af ringstedLC

#5
#3
$\small \begin{array}{llllll} \textup{beregning af }x\textup{:}\\& \begin{array}{llllll} (25-x)^2+12^2=25^2\quad \wedge\quad 0<x<25 \end{array} \end{array}$

Og er det muligt med en forklaring, om hvordan du har gjort dette? :D Beklager, jeg ikke lige forstår det helt

Det er også Pythagoras:

$\begin{align*} b^2+c^2 &= 25^2 \\ (25-x)^2+12^2 &= 25^2\wedge 0<x<25\,,\;b=25-x \\ x &=\;? \\ \text{Alternativt}: \\ x &= 25-B_y \end{align*}$

Brugbart svar (0)

Svar #9
20. september 2020 af ringstedLC

Figur til #7.

Vedhæftet fil:__0.png

Brugbart svar (0)

Svar #10
20. september 2020 af andre243g

#8
#5
#3
$\small \begin{array}{llllll} \textup{beregning af }x\textup{:}\\& \begin{array}{llllll} (25-x)^2+12^2=25^2\quad \wedge\quad 0<x<25 \end{array} \end{array}$

Og er det muligt med en forklaring, om hvordan du har gjort dette? :D Beklager, jeg ikke lige forstår det helt

Det er også Pythagoras:

$\begin{align*} b^2+c^2 &= 25^2 \\ (25-x)^2+12^2 &= 25^2\wedge 0<x<25\,,\;b=25-x \\ x &=\;? \\ \text{Alternativt}: \\ x &= 25-B_y \end{align*}$

Yes, har dog indelt den originale trekant til en retvinklede trekant, og dermed fundet y-koordinaten af punktet B.

Og fundet højden af x, ved at trække y-koordinaten fra radius, hvis dette også er muligt

Skriv et svar til: cirkel

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.