Matematik
Ligningssystem med 3 ligninger og 3 ubekendte
Hej folkens. Jeg har et ligningssystem jeg skal løse, og har stirret mig blindt. Fuld forventning til at det er nemt og jeg bare har misset det, men mine kammerater har samme problem.
For læsbarhed har jeg skrevet det ind i et latex program og vedhæftet et billede.
Vi at både x og y er positive hele tal.
På forhånd tak!
Svar #2
19. november 2020 af peter lind
1. løs den første ligning med hensyn til z og sæt det ind i den anden ligning. Derved får du en ligning, der kun er afhængig af x og y
2. Løs den tredje ligning med hensyn til y og sæt det ind i resultatet fra 1'. Derved får du en ligning, der kun afhænger af x
Svar #3
19. november 2020 af Capion1
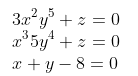
Det er jo ikke et lineært ligningssystem, så man kan isolere enten x eller y i (III) og
indsætte i (I) og (II) .
Læg mærke til, at summen af eksponenterne for x og y i (I) og (II) er ens.
En maskinløsning, når x og y skal være positive, er
(x , y , z) = (3 , 5 , - 84375)
Svar #4
19. november 2020 af Peter2235
Vi har forsøgt at indsætte en substitut for x i både (I) og (II) men ender med at sidde fast i begge før vi kommer til et "ordentligt" svar.
Nogen der har tid til at gennemgå en af dem? Ville vi sætte stor pris på.
Svar #5
19. november 2020 af Capion1
Man kan gennemgå de mulige værdier for x og y:
x y
1 7
2 6
3 5
4 4
5 3
6 2
7 1
Svar #6
19. november 2020 af Capion1
# 3 er for omstændelig.
3x2y5 = x3·5y4
Dividér på begge sider med x2y4
Svar #7
19. november 2020 af peter lind
du skal ikke indsætte et substitut for x. Gør som i #3. z = -3x2y5 og indsæt det i anden ligning
Skriv et svar til: Ligningssystem med 3 ligninger og 3 ubekendte
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.




