Matematik

Hvor mange sider har en polygon med 54 diagonaler?

09. januar 2021 af Alrighty - Niveau: B-niveau

En polygon med n sider har (1/2)n(n-3) diagonaler

Hvordan finder jeg ud af det?

Brugbart svar (0)

Svar #1
09. januar 2021 af Eksperimentalfysikeren

Der er n-1 liniestykker, der forbinder vinkel i en polygon med andre vinkler i polygonen. Ser man på den næste vinkel, er der igen n-1 liniestykker, men heraf har vi allerede talt den ene med, så der er kun n-2 "nye". Dete mønster følges hele vejen rundt. Det giver så summen (n-1) + (n-2) + ... + 1- Derfra skal trækkes de liniestykker, der ikke er diagonaler.

Brugbart svar (0)

Svar #2
09. januar 2021 af ringstedLC

#0: En polygon med 54 diagonaler har n sider:

$\begin{align*} \tfrac{1}{2}\cdot n\cdot (n-3) &= \text{Antal diagonaler}\;,\;n\in \mathbb{N}\setminus \left \{ 1;2 \right \} \\ \tfrac{1}{2}\cdot n\cdot (n-3) &= 54 \\ n&=\;?\,\text{sider} \end{align*}$

Svar #3
11. januar 2021 af Alrighty

#2 hvad betyder det der e og N du skriver?

Svar #4
11. januar 2021 af Alrighty

Jeg har prøvet at regne det ud således (vedhæftet fil) men metoden er nok ikke korrekt

Vedhæftet fil:nr12.png

Brugbart svar (0)

Svar #5
11. januar 2021 af ringstedLC

#3:

$\begin{align*} &n\;\underbrace{\in} &\underbrace{\mathbb{N}}\;\; &\qquad\quad\underbrace{\setminus \left \{ 1;2 \right \}}\qquad\qquad\qquad\qquad \\ &\quad\text{tilh.}& \text{Nat.\,tal}&\quad \text{minus\;m\ae ngden\;af...} \end{align*}$

Brugbart svar (0)

Svar #6
11. januar 2021 af ringstedLC

#4: Du skal bruge formlen til at løse ligningen:

$\begin{align*} \tfrac{1}{2}\, n\, (n-3) &= \text{diag.} \\ \tfrac{1}{2}\, n^2-\tfrac{3}{2}\, n &= \text{diag.} \\ n^2-3n &= 2\,\text{diag.} \end{align*}$

indsæt 54, træk 2 gg 54 fra på begge sider, så du får en 2. gradsligning på standardform.

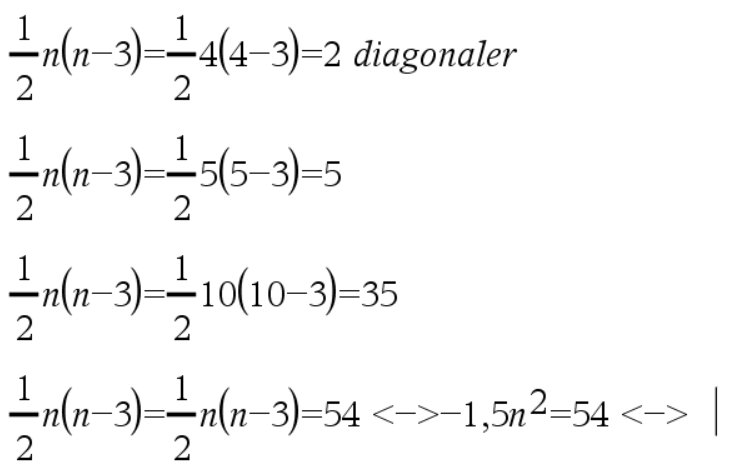
... og du skal gange rigtigt ind i parentesen.

Svar #7
12. januar 2021 af Alrighty

n²-3n=108

n²-3n-108=0

d=b²-4ac <-> d=(-3)²-4*1*(-108)=441

diskriminanten er over 0 hvilket kan give to løsninger: $x=\frac{-b\pm\sqrt{d}}{2a}$ Men polygonen med 54 diagonaler kan vel kun have ét specifikt antal sider?

Brugbart svar (0)

Svar #8
12. januar 2021 af ringstedLC

#7: Næsten korrekt. d > 0 ⇒ 2 løsninger. Men det er den slags små sten på vejen, man kan komme ud for ved at bruge en formel til noget andet, end den er beregnet til.

Derfor sættes betingelsen (kriteriet): n ∈ N \ {1;2} i #2. Løs ligningen og forkast den (de) løsning(er), der ikke opfylder betingelsen.

Betingelsen betyder, at polygonen skal have mindst 3 "hele" sider, hvilket jo er logisk. Men den gør også, at hvis du kommer med et "umuligt" antal diagonaler fx 53 (prøv selv), ja så må begge løsninger forkastes.

En tilsvarende eksempel: Arealet af en cirkel er 4π. Beregn radius.

Her bruges cirklens areal til bestemme r:

$\begin{align*} A &= \pi\,r^2 \\ \pi\,r^2 &= 4\pi \\ r^2 &= \tfrac{4\pi}{\pi} \\ r &= \pm \sqrt{4}=\pm2 \;,\,r > 0\Rightarrow r=2 \end{align*}$

Svar #9
12. januar 2021 af Alrighty

$\frac{-(-3)+\sqrt{441}}{2*1}$ =12 som også er resultatet i bogen. Jeg undrer mig, at ikke synes at kunne finde info om denne betingelse i min bog.

Jeg er dog lidt forvirret af \ {1;2}. Du skriver det betyder ''minus mængden af'', jeg læser det som noget divideret med x og y

Brugbart svar (0)

Svar #10
13. januar 2021 af ringstedLC

#9: Netop.

Vedr. betingelse: Fordi formlen normalt bruges til at beregne antallet af diagonaler er den unødvendig. Du ville jo fx aldrig sige n = 2 (polygoner har mindst 3 sider) eller n = 1.47. Men her bruges den omvendt og så er betingelsen nødvendig for at kunne forkaste de forkerte løsninger.

Jeg havde ellers håbet, at du kunne se fornuften i eksemplet med cirklen.

Vedr. "\": Et skråtstillet divisionstegn er "/". Alle naturlige tal, undtagen 1 og 2.

Skriv et svar til: Hvor mange sider har en polygon med 54 diagonaler?

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.