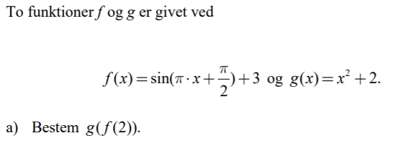Matematik

To funktioner

12. april 2021 af Sofie9802 - Niveau: B-niveau

Jeg sidder og prøver at lave vedhæftede opgave, men jeg ved simpelthen ikke hvordan jeg skal løse den, da den skal løses uden hjælpemidler, én der kan hjælpe.

Tak på forhånd

Vedhæftet fil: Opgave.PNG

Brugbart svar (0)

Svar #1
12. april 2021 af ringstedLC

Beregn f(2). Sæt resultatet ind i g(x).

Svar #2
12. april 2021 af Sofie9802

Så får jeg den til at give 1, skal jeg så sætte 1 ind på x's plads i g(x)?

Brugbart svar (0)

Svar #3
12. april 2021 af oppenede

Vis hvordan du får 1.

Brugbart svar (0)

Svar #4
12. april 2021 af ringstedLC

Njaeh, 1 + ... sættes ind i g.

Svar #5
12. april 2021 af Sofie9802

Jeg får den faktisk til at give 0.1366, men det gør jeg på en lommeregner, har ikke skrevet metoden op i hånden endnu, da jeg lige vil forstå selve opgaven, og hvordan jeg skal løse den.

Når jeg løser den i hånden får jeg den til at være lig 1..?

Svar #6
12. april 2021 af Sofie9802

$sin(\pi *2+\frac{\pi}{2}) \rightarrow sin(\frac{\pi}{2}) \rightarrow =1$

Brugbart svar (0)

Svar #7
13. april 2021 af ringstedLC

#5: Så var det jo ikke særligt smart at skrive som i #2.

Og den lommeregner er ikke noget værd eller også ved du ikke hvordan den skal betjenes. Brug hovedet og papiret

#6: OK, bestem så f(2)

Brugbart svar (1)

Svar #8
13. april 2021 af AMelev

#5 Du får 0.1366, fordi din lommeregner står til at regne i grader, men dette er i radian, da det er funktioner.

#6 sin er periodisk med perioden 2π (svarende til en runde på enhedscirklen).
Altså $sin(2\pi +\frac{\pi}{2})=sin(\frac{\pi}{2})=1$ , da $(\frac{\pi}{2})=90^{\circ}$ , så retningspunktet på enhedscirklen er (0,1)
Husk, at dette ikke er hele f.
$f(2) =sin(2\pi +\frac{\pi}{2})+3=4$ , som indsættes i g.

Skriv et svar til: To funktioner

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.