Matematik

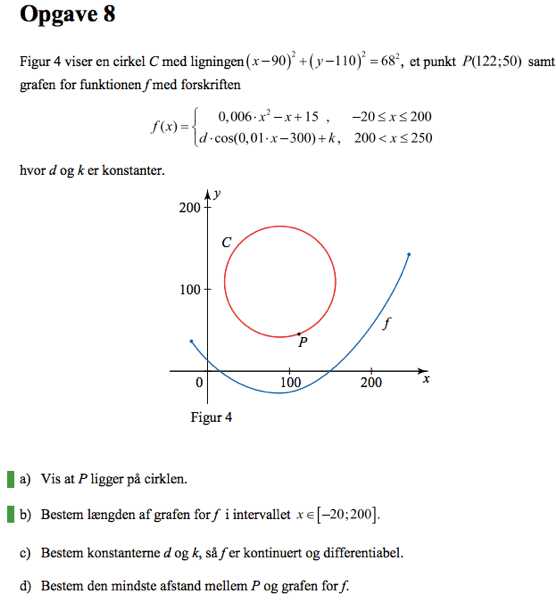
Bestem konstanterne d og k, så f er kontinuert og differentiabel

26. maj 2021 af Hmmma - Niveau: A-niveau

Hej,
nogle, der kan hjælpe med c) og d)?

Hvordan bestemmer jeg konstanterne d og k, så f er kontinuert og differentiabel?

Hvordan bestemmer jeg den mindste afstand mellem P og grafen for f?

På forhånd mange tak

Vedhæftet fil: Opgave 8.png

Brugbart svar (0)

Svar #1
26. maj 2021 af StoreNord

Differentièr f så k går ud, og bestem d ved at sætte de 2 dele af f' lig med hinanden.

Brugbart svar (0)

Svar #2
26. maj 2021 af StoreNord

Det skal være med x=200

Svar #3
26. maj 2021 af Hmmma

Hvordan går k ud, når jeg differentierer den? Har jeg gjort det rigtigt som på det vedhæftede billede?

Vedhæftet fil:Skærmbillede 2021-05-26 kl. 23.32.07.png

Brugbart svar (0)

Svar #4
26. maj 2021 af StoreNord

k går ud fordi du skal differentiere med hensyn til x.

Du skulle arbejde med f-mærke.

Det er vist forkert, at har indsat 200 før efter, at du har differentieret.

Brugbart svar (0)

Svar #5
29. maj 2021 af ringstedLC

$\begin{align*} \bigl(x-90\bigr)^2+\bigl(y-110\bigr)^2 &= 68^2 \\ \bigl(x_P-90\bigr)^2+\bigl(y_P-110\bigr)^2 &= 68^2 \end{align*}$

Brugbart svar (0)

Svar #6
29. maj 2021 af ringstedLC

Her gør du noget umuligt. Man kan ikke løse én ligning med to ubekendte. Desuden er din Wordmat indstillet til grader og ikke radianer.

For at f skal være kontinuert og differentiabel:

$\begin{align*} {f_1}'(200) &= {f_2}'(200)\Rightarrow d=\;? \\ f_1(200) &= f_2(200)\Rightarrow k= \;? \end{align*}$

Brugbart svar (0)

Svar #7
29. maj 2021 af ringstedLC

$\begin{align*} Q:&\bigl(x_Q,f(x_Q)\bigr)\quad\textup{et punkt p\aa\;}f \\ \textup{afst}(P,Q) &=\sqrt{(x_Q-x_P)^2+\bigl(f(x_Q)-y_P\bigr)^2} =... \\ \textup{afst}(x_Q) &= ...\Rightarrow \textup{afst}'(x_Q)=...\\ \textup{afst}'(x_Q) &= 0\Rightarrow x_0=\;? \\ \textup{afst}_{min}&=\textup{afst}(x_0)= \;? \end{align*}$

Skriv et svar til: Bestem konstanterne d og k, så f er kontinuert og differentiabel

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.