Matematik

Rekursiv formel

29. august 2021 af Mathian - Niveau: Universitet/Videregående

Hej venner.

Jeg skal have opstillet en rekursiv formel, og er på jagt efter en god forklaring og nogle principper jeg kan tage med mig. Det ville være en rigtig stor hjælp

Vedhæftet fil: Skærmbillede 2021-08-29 kl. 20.41.21.png

Brugbart svar (0)

Svar #1
29. august 2021 af StoreNord

Prikken til venstre, skal den bruges til noget?

Svar #2
29. august 2021 af Mathian

Det må vel være starten tænker jeg

Brugbart svar (0)

Svar #3
29. august 2021 af StoreNord

Er det ikke et kvadrattal i midten, og trekanttal i toppen og til hver side?

Brugbart svar (0)

Svar #4
29. august 2021 af StoreNord

Mener du første skib?
Altså at der er 4 skibe?

Svar #5
29. august 2021 af Mathian

Ved ikke om man kan kalde det et skib, det er jo bare fire figurer som vokser med et bestemt antal prikker. Jeg skal så opstille en rekursiv formel.

Brugbart svar (0)

Svar #6
29. august 2021 af Soeffi

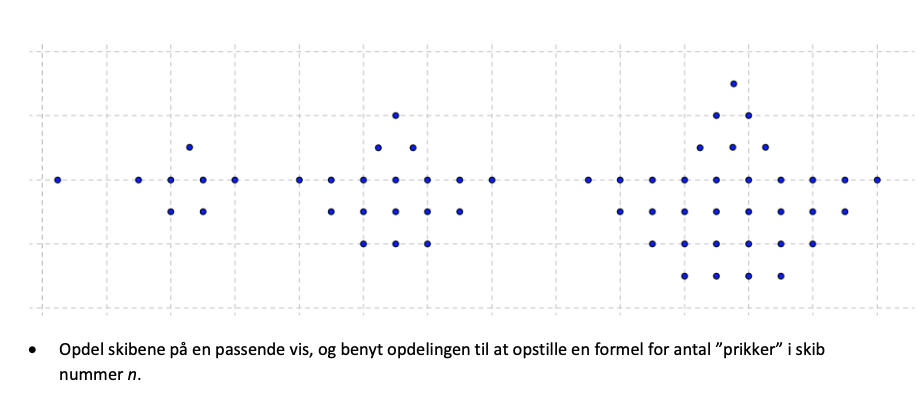
#0. Hvis du inddeler figurerne, så kan du få trekanter og firkanter dermed bl.a. bruge trekantstallene.

Brugbart svar (0)

Svar #7
29. august 2021 af oppenede

Jeg kan ikke se nogen oplagt rekursiv formel, men det er oplagt at opdele efter hver række i to grupper af rækker. Lad n=0 svare til den første med 1 prik.

Dermed har det n'te skib øverst n rækker med 1, 2, ..., n prikker i hver række oppefra
$\sum _{j=1}^n j$
Nederst har det n'te skib n+1 rækker med n+1 prikker nederst og 2 ekstra pr. række opad
$\sum _{i=0}^n (n+1+2 i)$

Brugbart svar (0)

Svar #8
29. august 2021 af SuneChr

a_n = (5n² - 3n)/2 n = 1, 2, ...

Brugbart svar (0)

Svar #9
29. august 2021 af SuneChr

$a_{n+1}=\frac{\left ( n+1 \right )\left ( 5n+2 \right )}{n\left ( 5n-3 \right )}a_{n}$ n = 1, 2, ...

Brugbart svar (0)

Svar #10
30. august 2021 af SuneChr

Man kan gøre det på flere måder.
- Kvadrat plus tre trekanter á lige mange prikker.
Single-prikken til venstre er måske ikke lige til at få ind i familien.
- Jeg har gjort dét i # 8, at opstille tre andengradsligninger med tre ubekendte. Det er et meget godt trick
i lignende opgaver. Man skal naturligvis forvisse sig om, at algoritmen vil holde for alle naturlige tal n.
# 9 er fremkommet ved simpel division a_{n + 1}/a_n

Brugbart svar (0)

Svar #11
31. august 2021 af Soeffi

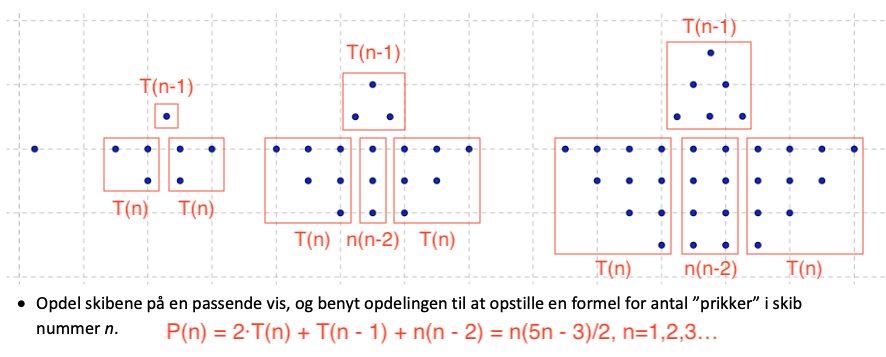
#0. Forslag hvor P(n) er antallet af prikker i n-te figur og T(n) er det n-te trekantstal:...

Vedhæftet fil:2020325.png

Brugbart svar (0)

Svar #12
31. august 2021 af Soeffi

#10...Jeg har gjort dét i # 8, at opstille tre andengradsligninger med tre ubekendte...

Det er vel tre førstegradsligninger, når det kommer til stykket(?):

$\left\{\begin{matrix} a\cdot 2^2+b\cdot 2+c=7 \phantom{..} \\a\cdot 3^2+b\cdot 3+c=18 \\ a\cdot 4^2+b\cdot 4+c=34 \end{matrix}\right.$ $\Rightarrow \left\{\begin{matrix} 4a +2b+c=7 \phantom{...} \\9a+3b+c=18\phantom{.} \\ 16a+4b+c=34 \end{matrix}\right.$ $\Rightarrow \left\{\begin{matrix} a = 5/2 \phantom{....} \\b = -3/2\phantom{.} \\ c = 0 \phantom{........}\end{matrix}\right.$

Skriv et svar til: Rekursiv formel

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.