Matematik

Hvordan løser jeg b) ?

22. september 2021 af Uduelig - Niveau: A-niveau

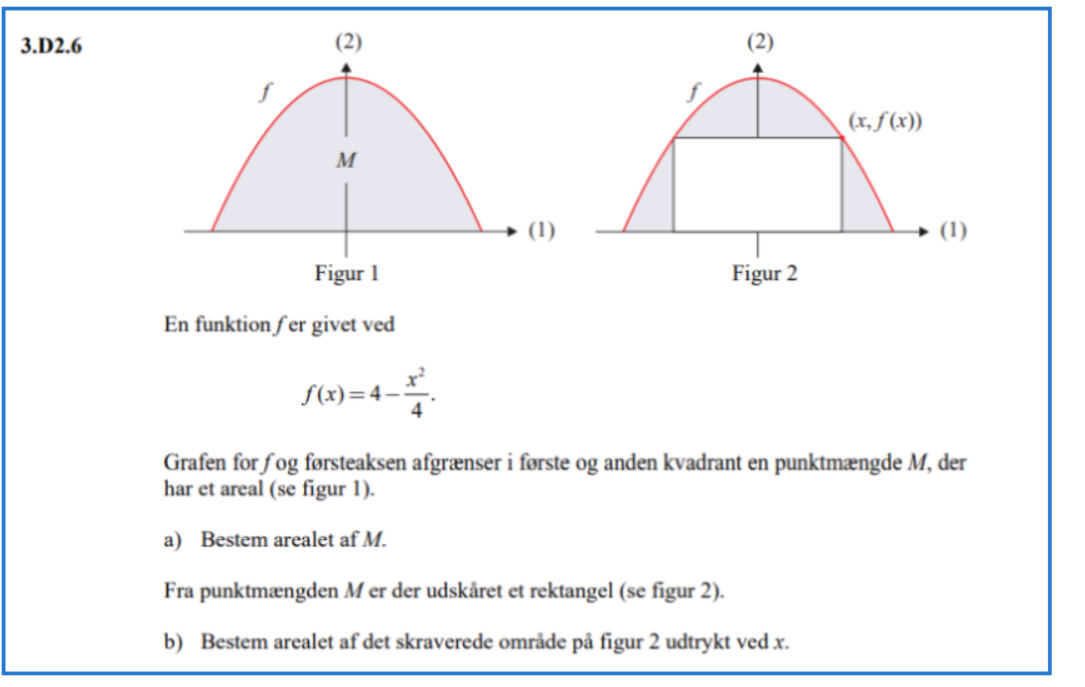
Titel. Jeg har tænkt over det, og ved ikke rigtigt hvilket måde jeg burde gribe det an på. Jeg har vedhæftet filen.

Vedhæftet fil: Skærmbillede 2021-09-22 042529.png

Brugbart svar (1)

Svar #1
22. september 2021 af mathon

Brugbart svar (1)

Svar #2
22. september 2021 af mathon

Først findes parablens nulpunkter:

$\small \begin{array}{llllll}&& 4-\frac{x^2}{4}=0\\\\&& 16-x^2=0\\\\&& x=\left\{\begin{matrix} -4\\4 \end{matrix}\right. \end{array}$

$\small \begin{array}{llllll}\textbf{a)}\\&& A_M=&2\cdot \int_{0}^{4}\left ( 4-\frac{1}{4}x^2 \right )=2\cdot \left [4x-\frac{1}{4\cdot 3}x^3 \right ]_0^{4}=2\cdot \left ( 4^2-\frac{1}{4\cdot3}\cdot 4^3 \right )=\\\\&&& 2\cdot 4^2\cdot \left ( 1-\frac{1}{3} \right )=32\cdot \frac{2}{3}=\frac{64}{3}=\frac{63}{3}+\frac{1}{3}=21\frac{1}{3} \end{array}$

Det bemærkes, at rektanglet også er symmetrisk om y-aksen.

.
$\small \begin{array}{llllll}\textbf{b)}\\&& A_{\textup{skraveret}}=&2\cdot \left ( \frac{32}{3}-x\cdot f(x) \right ) =2\cdot \left ( \frac{32}{3}-x\cdot \left ( 4-\frac{1}{4}\cdot x^2 \right ) \right )=\\\\&&& 2\cdot \left ( \frac{32}{3}-4x+\frac{1}{4}x^3 \right )=\frac{1}{2}x^3-8x+\frac{64}{3} \end{array}$

Brugbart svar (1)

Svar #3
22. september 2021 af Soeffi

#0. Se evt. https://www.studieportalen.dk/forums/thread.aspx?id=1910318.

Skriv et svar til: Hvordan løser jeg b) ?

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.