Matematik

Areal af tetreader ud fra ingen fælles punkter

14. oktober 2021 af Thifo1507 - Niveau: Universitet/Videregående

Hej.

Jeg er gået i stå i opgave b, da jeg har virkelig svært ved at se hvordan jeg skal udregne areal ud fra en ligningssystem, som har ingen løsning. Dog ved jeg at en ingen løsning = ingen fælles punkter, og det svarer selvfølgelig til en tetreader, som nævnt i opgaven. Og jeg ved også, at man kan udregne areal ved hjælp af determinat eller krydsprodukt, men jeg kan simpelthen ikke finde ud af hvordan jeg skal gå fra en ligningsystem, hvor resultatet er (x,y,z)=(0,0,-1) og den sidste ligning er 0=6 og så til at udregne areal.

Håber i kan hjælpe!

Vedhæftet fil: hjemmeopgavesæt 2 opgave 3.png

Brugbart svar (0)

Svar #1
14. oktober 2021 af Soeffi

#0. Indsætter billede...

Svar #2
14. oktober 2021 af Thifo1507

Tak :-D

Brugbart svar (0)

Svar #3
14. oktober 2021 af Soeffi

#0. a) Man opstiller og reducerer ligningsmatricen:

$A=\begin{bmatrix} 1 & -2 & -1 & 1\\ 1 & 0 & 1 & -1\\ -1 & -1 & 1 & -1\\ 1 & -1 & -3 & k \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & -1\\ 0 & 0 & 0 & 3-k \end{bmatrix}$

Heraf fremgår det, at der ikke er løsninger for k ≠ 3, og at løsningen for k = 3 er (x,y,z) = (0,0,-1).

b) Man skal regne de punkter ud som den fjerde plan har tilfælles med hvert par af de andre planer. (Man ved fra opgaven, at disse punkter eksisterer).

Man beregner først det punkt, som fjerde plan har til fælles med plan 1 og 2:

$A_{124}=\begin{bmatrix} 1 & -2 & -1 & 1\\ 1 & 0 & 1 & -1\\ 1 & -1 & -3 & 9 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & 2\\ 0 & 1 & 0 & 2\\ 0 & 0 & 1 & -3 \end{bmatrix}$

På tilsvarende måde beregnes de to andre punkter for siden af tetraederet i plan 4:

$A_{134}=\begin{bmatrix} 1 & -2 & -1 & 1\\ -1 & -1 & 1 & -1\\ 1 & -1 & -3 & 9 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & -3\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & -4 \end{bmatrix}$

$A_{234}=\begin{bmatrix} 1 & 0 & 1 & -1\\ -1 & -1 & 1 & -1\\ 1 & -1 & -3 & 9 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & 1\\ 0 & 1 & 0 & -2\\ 0 & 0 & 1 & -2 \end{bmatrix}$

Man har nu punkterne P = (2,2,-3), Q = (-3,0,-4) og R = (1,-2,-2). Arealet af siden kan beregnes som:...

$\frac{1}{2}\cdot \left | \overset{\rightarrow}{PQ} \times \overset{\rightarrow}{PR} \right |$

c.1) Fra spørgsmål a) kender man det punkt i tetraederet, der ikke ligger i plan 4, nemlig: S = (0,0,-1).

Rumfanget beregnes med en af følgende formler (rumproduktformel og determinantformel):

$\frac{1}{6}\cdot \left |\left ( \overset{\rightarrow}{PQ} \times \overset{\rightarrow}{PR} \right )\cdot \overset{\rightarrow}{PS} \right | = \frac{1}{6}\cdot \left | det \begin{pmatrix} x_P& y_P & z_P & 1\\ x_Q & y_Q & z_Q & 1\\ x_R & y_R & z_R & 1\\ x_S & y_S & z_S & 1\\ \end{pmatrix} \right |$

c.2) Hvis jeg beholder k i beregningen af P, Q og R, så får jeg:

$P=\begin{pmatrix} k/3-1\\ k/3-1\\ -k/3 \end{pmatrix}, \; Q=\begin{pmatrix} 3/2-k/2\\ 0\\ 1/2-k/2 \end{pmatrix} \;og\;R= \begin{pmatrix} k/6-1/2\\ 1-k/3\\ -k/6-1/2 \end{pmatrix}$

Hvis man herefter bruger determinantformlen til at finde rumfanget, så vil man få en fjerdegradsligning i k, som kan løses i Maple. (Jeg har ikke prøvet).

d) Følgende tegning er lavet i Geogebra:

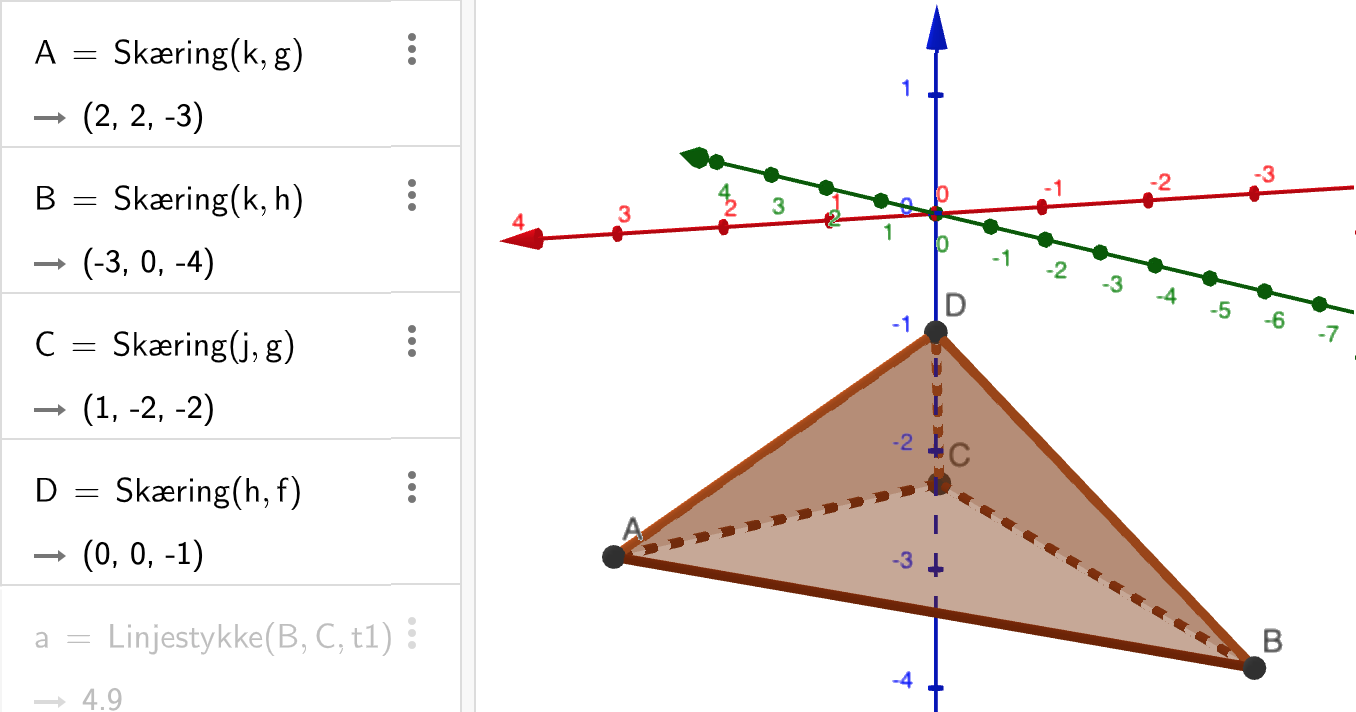
Vedhæftet fil:Skærmbillede 2021-10-14 kl. 18.19.09.png

Svar #4
14. oktober 2021 af Thifo1507

Jeg fandt også endelig ud af det i opgave b, men tusind TUSIND tak for hjælpen alligevel!! :-D

Brugbart svar (0)

Svar #5
15. oktober 2021 af Soeffi

#0. Søgeord: Lineær algebra, matrix, rumgeometri, plan, teraeder, vektor, krydsprodukt, determinant, Maple.

Se også: https://www.studieportalen.dk/forums/thread.aspx?id=1979458 og

https://www.studieportalen.dk/forums/thread.aspx?id=1916098.

Skriv et svar til: Areal af tetreader ud fra ingen fælles punkter

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.