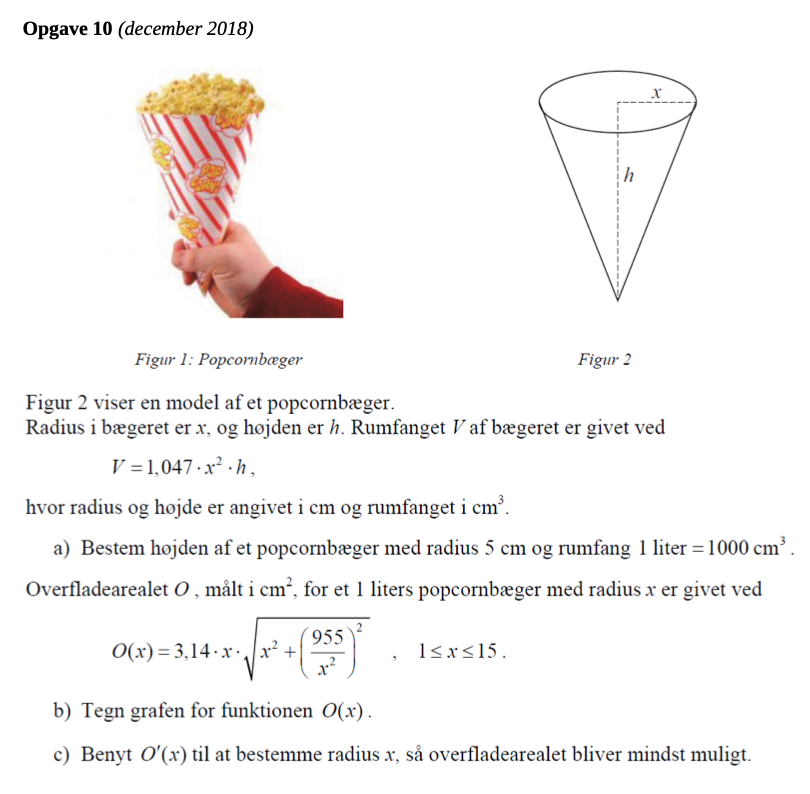
Matematik
Bestem højden af et popcornbæger med radius 5 cm og rumfang 1 liter = 1000 cm3
25. oktober 2021 af
maya1999
-
Niveau: B-niveau
Hej har en aflevering for til i aften, og kan ikke finde ud af denne opgave eller hvordan man taster det ind i wordmat, så hvis der er nogen der kan hjælpe vil det være meget værdsat
Vedhæftet fil: Skærmbillede 2021-10-25 kl. 09.17.29.png
Svar #3
25. oktober 2021 af maya1999
Tusind tak for hjælpen! Kan godt løse a nu og tak for at hjælpen med c.
Er det her svaret på opgave b)?
Vedhæftet fil:Skærmbillede 2021-10-25 kl. 11.15.39.png
Skriv et svar til: Bestem højden af et popcornbæger med radius 5 cm og rumfang 1 liter = 1000 cm3
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.