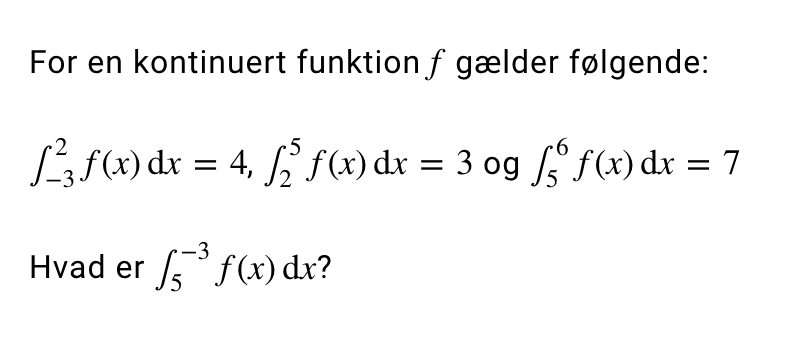Matematik

Bestem det ubestemte integrale

02. oktober 2022 af Guleroden1 - Niveau: A-niveau

Hvordan skal jeg gribe denne her opgave an?

Vedhæftet fil: Skærmbillede 2022-10-02 kl. 12.48.21.png

Brugbart svar (0)

Svar #1
02. oktober 2022 af mathon

Brugbart svar (0)

Svar #2
02. oktober 2022 af mathon

Mon ikke spørgsmålet
er
$\int_{-3}^{5}f(x)\, \mathrm{d}x\; ?$

Brugbart svar (0)

Svar #3
02. oktober 2022 af ringstedLC

#0:

$\begin{align*} \int_{-3}^{2}\!f(x)\,\mathrm{d}x=F(2)-F(-3) &= 4 \\ F(-3) &= F(2)-4 \\ \int_{2}^{5}\!f(x)\,\mathrm{d}x=F(5)-F(2) &= 3 \\ F(5) &= 3+F(2) \\ \int_{5}^{-3}\!f(x)\,\mathrm{d}x &= ... \end{align*}$

NB: Opdatér din profil

Brugbart svar (0)

Svar #4
02. oktober 2022 af ringstedLC

"Bestem det ubestemte integrale", - opgaven handler om et bestemt integral.

Svar #5
02. oktober 2022 af Guleroden1

Hvordan ved jeg hvad f(x) er? forstår ikke

Brugbart svar (0)

Svar #6
02. oktober 2022 af ringstedLC

#5: Det behøver du ikke at vide. Se at:

$\begin{align*} \int_{5}^{-3}\!f(x)\,\mathrm{d}x &= F(-3)-F(5) \\&=... \end{align*}$

Svar #7
03. oktober 2022 af Guleroden1

#6
#5: Det behøver du ikke at vide. Se at:

$\begin{align*} \int_{5}^{-3}\!f(x)\,\mathrm{d}x &= F(-3)-F(5) \\&=... \end{align*}$

Så det giver -8? hvordan beregner jeg det der

Brugbart svar (0)

Svar #8
03. oktober 2022 af ringstedLC

-8; fordi -3 - 5 = -8 Nej.

Genlæs #3 og tænk over, hvorfor mon F(-3) og F(5) isoleres...

Resultatet er -7.

Brugbart svar (0)

Svar #9
03. oktober 2022 af SuneChr

Sidste linje i det vedhæftede:
Det er let at indse, at
_a∫^b f = - _b∫^a f
Venstresiden: F(b) - F(a)
Højresiden: - (F(a) - F(b)) = F(b) - F(a)

Skriv et svar til: Bestem det ubestemte integrale

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.