Matematik
augmenter at trekanterne har samme areal
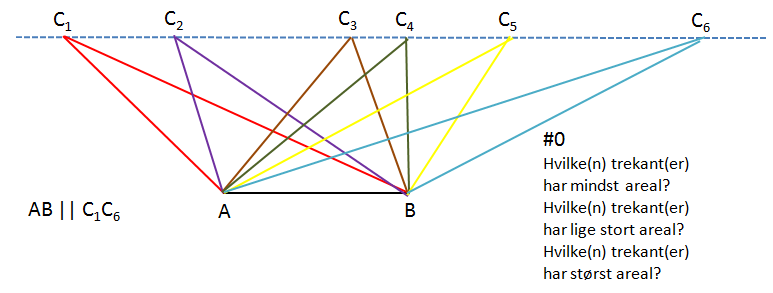
hej jeg har et dumt spørgsmål. jeg har i geogebra fundet ud af at de to trekanter har samme areal på præsis 24,62019 men hvordan agumentere jeg for det som opgave b på det vedhæfte billede siger jeg skal?
ps der er et par fejl i opgaveformeleringen det er trekant ABM og ikke ACM der skal agumenteres for
på forhånd tak for hjælpen :)
Svar #1
20. november 2022 af MentorMath
Hej. Man kan argumentere for, at de to trekanter har samme areal, da de to trekanter ABM og BCM har samme højde, og deres grundlinjer er lige store :))
Svar #4
20. november 2022 af StoreNord
Du må aldrig sammenligne to decimaltal.
De kan være forskellige, lige meget hvor mange decimaler du tager med.
Svar #7
21. november 2022 af chapman
så ved jeg ikke hvad jeg skal gøre for det er arealet af trekanterne så kan selvfølgelig godt runde op eller ned men ellers kan jeg jo ikke ændre på noget
Svar #8
21. november 2022 af StoreNord
For at beregne om to arealberegninger giver præcis samme facit skal du skrive dem som brøker og uden komma. Skriv dem i en ligning, som
Brøk1 = Brøk2.
Gang så tæller med nævner og nævner med tæller på kryds hen over lighedstegnet.
Hvis det giver samme tal på hver side (og uden komma), var ligningen sand og arealerne ens.
Svar #9
24. november 2022 af chapman
Svar #10
25. november 2022 af SuneChr
Skal man afgøre, om to reelle tal er ens, kan man sammenligne to rationale tal .
Hvis p1 = p2 og q1 = q2 , når de er uforkortelige, så er de to tal ens.
Arealet af ΔABC er 1/2·10·cos 40º·10·sin 40º = 25·sin 80º
Det halve areal er 25/2·sin 80º = 12,310096...
men højre side er k u n lig med venstre side, hvis decimalrækken løber uden grænse.
Man kan udvikle en række med denne grænseværdi, men det ligger ud over nærværende pensum.
Skriv et svar til: augmenter at trekanterne har samme areal
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.