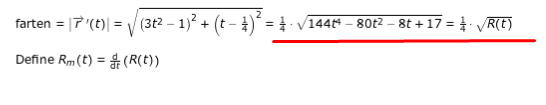Matematik

Opgave om vektorfunktioner - Bestem længden af hastighedsvektoren som funktion af t

22. november 2022 af Silvia77 - Niveau: A-niveau

Hej

jeg er helt stucket med den her opgave, del e. De andre dele kunne jeg godt svare (del c svarede jeg på en lidt for kreative form, men jeg gider ikke at ligge mere tid på den):

Brugbart svar (0)

Svar #1
22. november 2022 af MentorMath

Hej, tror ikke du har vedhæftet opgaven..? :)

Svar #2
22. november 2022 af Silvia77

Jeg glemte at oploade billedet med opgavens beskrivelse

Vedhæftet fil:Screenshot_1.jpg

Brugbart svar (0)

Svar #3
22. november 2022 af MentorMath

Okay, kan godt se opgaven nu.

Brugbart svar (0)

Svar #4
22. november 2022 af mathon

Brugbart svar (0)

Svar #5
22. november 2022 af MentorMath

Jeg går ud fra, at man kan løse e) på følgende måde(har vedhæftet et bilag). I så fald er der nok en anden herinde, der kan korrigere eller uddybe svaret til løsningen yderligere.

Vedhæftet fil:316103391_1178133343083861_4610761229283329125_n.jpg

Brugbart svar (0)

Svar #6
22. november 2022 af mathon

$\small \begin{array}{lllllll} \textbf{e)}\\&& \overrightarrow{r}{\, }'(t)=\begin{pmatrix} 3t^2-1\\t-\frac{1}{4} \end{pmatrix}\\\\&& \left | \overrightarrow{r}{\, }'(t) \right |=\sqrt{\left ( 3t^2-1 \right )^2+\left (t-\frac{1}{4} \right )^2}=\frac{1}{4}\cdot \sqrt{144t^4-80t^2-8t+17} \end{array}$

Brugbart svar (0)

Svar #7
22. november 2022 af mathon

$\small \small \begin{array}{lllllll} \textbf{e)}\\&& \overrightarrow{r}{\, }'(t)=\begin{pmatrix} 3t^2-1\\t-\frac{1}{4} \end{pmatrix}\\\\&&\textup{farten}= \left | \overrightarrow{r}{\, }'(t) \right |=\sqrt{\left ( 3t^2-1 \right )^2+\left (t-\frac{1}{4} \right )^2}=\frac{1}{4}\cdot \sqrt{144t^4-80t^2-8t+17}=\frac{1}{4}\cdot \sqrt{R(t)}\\\\&&\textup{Define }R_m(t)=\frac{\mathrm{d} }{\mathrm{d} t}\left ( R(t) \right )\\\\& \textup{mindste fart}\\&\textup{kr\ae ver bl.a.}\\&&Rm(t_o)=0\\\\&&t_o=\begin{pmatrix} -\frac{1}{2}\\ \frac{3-\sqrt{13}}{12} \\ \frac{3+\sqrt{13}}{12} \end{pmatrix}\\\\&\textup{Af fortegns-}\\&\textup{variationen for }fm(t)\\&\textup{ses, at} \\\\& Rm(t)\textup{ og dermed farten}\\&\textup{har minimum for }\\&&t_o=\frac{3+\sqrt{13}}{12}\\\\&\textup{Mindste fart:}\\&&\left | \overrightarrow{r}{\, }'(\frac{3+\sqrt{13}}{12}) \right |=\frac{1}{4}\cdot \sqrt{R\left ( \frac{3+\sqrt{13}}{12} \right )}=0.313933 \end{array}$

Svar #8
23. november 2022 af Silvia77

jeg bliver stoppet her

betyder det at man definerer hele kvadratrodet som R(t) ?
hvad er Rm?

Brugbart svar (0)

Svar #9
23. november 2022 af mathon

$\small \begin{array}{lllllllll} \sqrt{{\color{Red} R(t)}}=\sqrt{{\color{Red} 144t^4-80t^2-8t}}\\\\ Rm(t)=R{\, }'(t)\quad \left ( Rm(\ae rke) \; af\; t \right ) \end{array}$

Skriv et svar til: Opgave om vektorfunktioner - Bestem længden af hastighedsvektoren som funktion af t

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.