Matematik
Akut brug for hjælp (integralregning)!!
Hej venner, jeg er i gang med en aflevering til på søndag. Jeg er desværre stået fast i en opgave, og har virkelig prøvet mig frem, men kan ikke løse den. Den første delopgave har jeg løst, men kan ikke finde ud af den anden delopgave, hvilket lyder således: Bestem arealet af hvert af områderne M2 og M3. Opgaven er vedhæftet.
Håber i kan hjælpe:)
Svar #2
22. november 2022 af Hansatios
Hej Sandra03,
Specificeres der, om M2 og M3 skal løses ved hjælp af stamfunktionen eller er det kun M1?
Mvh Hans
Svar #4
22. november 2022 af Sandra03
Hej #2, ift. dit spørgsmål, så bliver der ikke specificeret, om M2 og M3 skal løses ved hjælp af stamfunktionen. Jeg har forstået det som, at det skal løses vha. M1.
Svar #6
22. november 2022 af Sandra03
Hej #3, hvis jeg sætter F(x) ind i formlen int(f(x), x = a .. b), så får jeg et negativt tal. Jeg har i stedet indsat f(x) ind og bestemt dens bestemte integral, givet at vi har en øvre grænse 4 og en nedre grænse 1. Når jeg integrerer udtrykket får jeg resultatet 6.44. Ved ikke om det er rigtigt, og hvis det ikke er, så vil jeg meget gerne høre en forklaring på det:)
Svar #8
22. november 2022 af Hansatios
Okay,
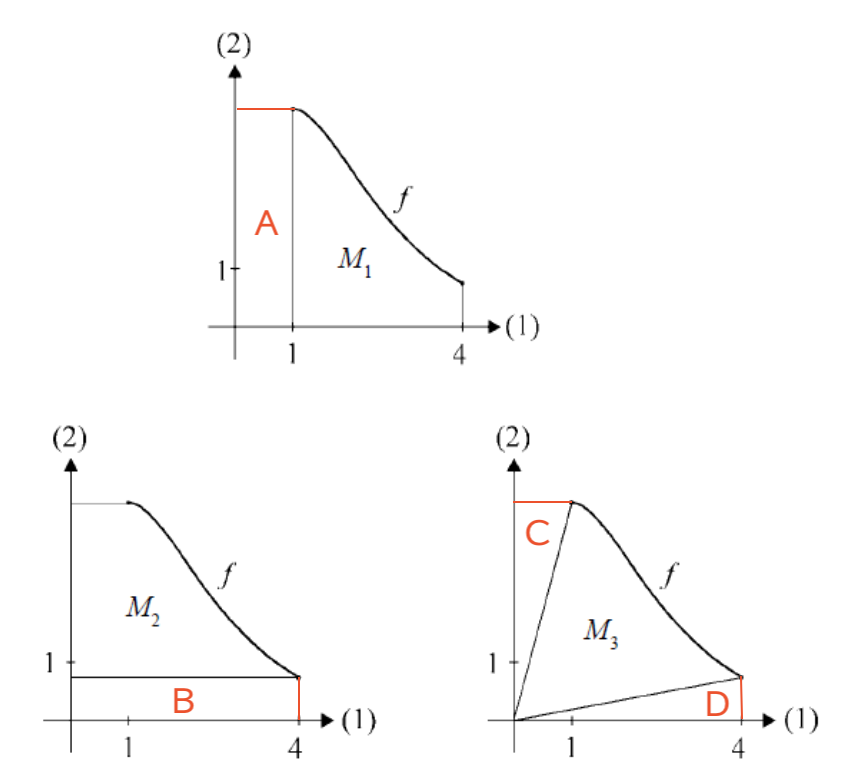
Jeg vil anbefale i M2 at åbne GeoGebra eller et andet CAS-værktøj, så du kan finde hvad f(1) og f(4) er. Så kan du gange 1 med længden af y-aksen der er mellem f(1) og f(4). Husk også at trække arealet mellem 1 og 4 fra arealet du fandt tidligere. Forestil dig der er to rektangler som beskrevet.
Hvad angår M3 vil jeg igen bruge GeoGebra, tegne grafen ind, og igen på trukket arealet langs x-aksen fra. Derefter vil jeg tegne en vandret og lodret linje, der skærer 1 og f(4). Brug polygonværktøjet. Slutproduktet skulle være noget i retning af den vedlagte screenshot jeg har lagt ind. Jeg håber det hjalp :)
~Hans
Svar #9
22. november 2022 af Sandra03
#7 Tak mathon, jeg forstår ikke, hvordan jeg skal bruge disse tal til at finde arealet. Håber du også kan hjælpe med det. Er i øvrigt meget taknemmelig for hjælpen:)
Svar #10
22. november 2022 af Sandra03
#8 Tak Hansatios, det er en kæmpe hjælp. Efter at have løst delopgave 1 (som jeg ikke har løst rigtigt :/) kan jeg gå videre via. din grundige forklaring. Tak:)
Svar #11
22. november 2022 af Sandra03
#7 Tror jeg har forstået det nu. Differensen F(4) - F(1) er svarende til arealet af M1?
Svar #12
22. november 2022 af Anders521
#11 Er det meningen, at opgaven skal løses med et CAS-værktøj?
Svar #13
22. november 2022 af Sandra03
#12 Ja, opgaven skal løses med maple. Jeg har via. maple CAS fået arealet til M1 at være 6.44
Svar #14
22. november 2022 af Anders521
#13 Men er det den eksakte værdi, som der efterspørges i opgaven?
Svar #16
22. november 2022 af SuneChr
Benyt integralregning til beregning af punktmængden
{(x , y) | 1 ≤ x ≤ 4 ∧ 1 ≤ y ≤ f (x)}
De tillagte arealer på M1 , M2 og M3 beregnes v.h.a. almindelig lineær geometri.
Pak al den elektronik væk og få hellere en forståelse af gammelt, sundt matematisk håndværk.
Svar #17
22. november 2022 af Soeffi
#0. På nedenstående tegning ses, at M2 = A + M1 - B og M3 = A + M1 - C - D.
Svar #18
23. november 2022 af SuneChr
Man kan af skitsen falde i fristelse til at tro, at
Areal A = Areal B = Areal (C + D)
Men da f (1) = 10/e ≠ 4 og f (4) = 40/e4 ≠ 1
må man konvertere sin tro til viden.
: )
Skriv et svar til: Akut brug for hjælp (integralregning)!!
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.










