Matematik

definitionsmængde af funktioner af flere variable

04. oktober 2023 af Elna2 - Niveau: Universitet/Videregående

Betragt funktionen f (x, y) = (2xy − x2)^1/2.

(funktionen er under kvadrat af to)
(a) Bestem definitionsmængden Df , dvs. den største mængde i xy-
planen hvor funktionen f er veldefineret. Skitser (evt. ved h °andtegning)
Df i xy-planen.

hvordan finder man difinationsmængden af funktioner af to variable? hvad er det jeg skal være opmærksom på?

Brugbart svar (0)

Svar #1
04. oktober 2023 af jl9

Tilhører værdimængden af f R?

Brugbart svar (0)

Svar #2
04. oktober 2023 af mathon

$\small \small \begin{array}{llllll} f(x,y)=\sqrt{2\cdot x\cdot y-x^2},\qquad 2\cdot x\cdot y-x^2 \geq 0 \end{array}$

Brugbart svar (0)

Svar #3
04. oktober 2023 af StoreNord

Vedhæftet fil:Definitionsmængde.png

Svar #4
04. oktober 2023 af Elna2

jeg har tænkt det samme at $2xy-x^2 >0$ , fordi man kan ikke sætte negative værdier ind pga. kvadratroden og -x^2 vokser hurtigere og har en negative fortegn. men er det ikke noget med R^2? hvornår er det at man siger definitionsmængde er R^2?

Brugbart svar (0)

Svar #5
04. oktober 2023 af M2023

#0. Det som står under kvadratroden skal være større end eller lig med 0.

$2xy-x^2\geq 0\Leftrightarrow x \cdot (2y-x)\geq 0\Leftrightarrow$

$(x\geq 0 \wedge (2y-x)\geq 0)\vee (x< 0 \wedge (2y-x)< 0)\Leftrightarrow$

$(x\geq 0 \wedge y\geq 0,5x)\vee (x< 0 \wedge y< 0,5x)$

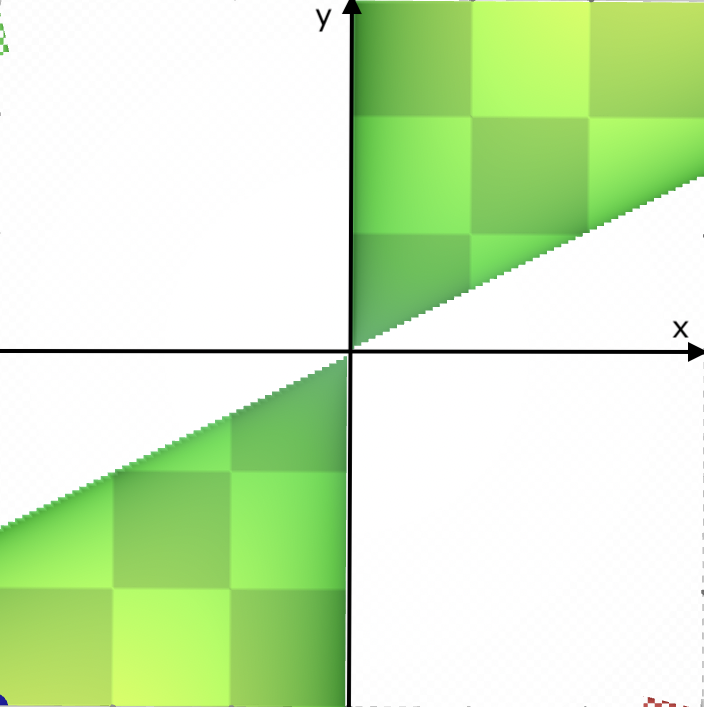
Set vinkelret på xy-planen fra den positive del af z-aksen.

Vedhæftet fil:dfmængde.png

Svar #6
04. oktober 2023 af Elna2

hvorfor min tegning ser anderledes ud????

Vedhæftet fil:Screenshot 2023-10-04 191424.png

Brugbart svar (0)

Svar #7
04. oktober 2023 af jl9

#6 behøver egentlig ikke tegne z-aksen eller også bare se det "oppefra"

https://www.google.com/search?q=sqrt(2*x*y-x%5E2)

Svar #8
04. oktober 2023 af Elna2

okay. men problemet er at der står at jeg skal tegn den med hånden. betyder det så at jeg skal bare vælge tilfældig x og y værdier? og tegn dem i en (x,y,z) plan? hvor z er resultatet af funktionen?

Brugbart svar (0)

Svar #9
04. oktober 2023 af jl9

skal lige nærlæse det forfra

Svar #10
04. oktober 2023 af Elna2

og igen i forhold til difinationsmængden har jeg fundet ud af at $y\neq 0$ fordi så er kvadratrodroden af $(-x^2)$ tilbage. kan det ikke pas?

Brugbart svar (0)

Svar #11
04. oktober 2023 af jl9

hvad er x?

Svar #12
04. oktober 2023 af Elna2

$\sqrt{2xy-x^2 }$ vi skulle jo finde difinationsmængde, jeg er med på at $2xy-x^2\geq 0$ men jeg tænker at 0 skal ikke være en del af difinationsmængde fordi hvis man sætter nul i y-plads så bliver funktionen $\sqrt{-x^2}$ , er vi enig?

det vil sige at difintionsmængden er $2xy-x^2> 0$ hvilket betyder at 0 er ikke med

Brugbart svar (0)

Svar #13
04. oktober 2023 af jl9

nå ja, du har ret! y kan ikke være 0

Svar #14
04. oktober 2023 af Elna2

fordi jeg har prøvet at tegne funktioen med hånden som opgaven siger.

1. ved at sætte y lig med nul og har givet funktionen forskellige x værdier.

2. ved at sætte x lig med nul og har givet funktionen forskellige y-værdier.

3- ved at sætte hele funktionen lig med en konstant og har givet funktionen forskellige x og y værdier.

så kan jeg tegne punkterne på en x,y,z plan.

Svar #15
04. oktober 2023 af Elna2

men 0 er ikke en del af difinationsmængde så jeg prøver lig med et andet tal

Brugbart svar (1)

Svar #16
04. oktober 2023 af jl9

#5 svar ser interessant ud

Brugbart svar (0)

Svar #17
04. oktober 2023 af M2023

#16. Tak. #5 bygger på reglen: a·b > 0 ⇔ (a > 0 ∧ b > 0) ∨ (a < 0 ∧ b < 0), hvilket vil sige, at et produkt er større end 0, hvis begge faktorer er positive eller hvis begge faktorer er negative.

Svar #18
04. oktober 2023 af Elna2

jeg har fx prøvet at x=3 og y=1 så fik jeg at $\sqrt{2*3*1-3^2}=\sqrt{-3}$ jeg ved ikke om det er mig der har misforstået difinationsmængden.

Svar #19
04. oktober 2023 af Elna2

man skal vælge y værdier der er meget større end x, fordi der står $x^2$ med en minus fortegn, det vil sige at den vokser meget hurtigere end y.

Brugbart svar (0)

Svar #20
04. oktober 2023 af M2023

#18...jeg har fx prøvet at x=3 og y=1 så fik jeg at $\sqrt{2*3*1-3^2}=\sqrt{-3}$ ...

Prøv at forklare hvad dette betyder:

#5...
$x\geq 0 \wedge y\geq 0,5x$

Forrige 1 2 Næste

Der er 28 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.