Matematik
Krav for differentiabel funktion
Er der flere krav for at en funktion skal være differentiabel, end at den skal være kontinuer?
Svar #1
15. november 2023 af oppenede
Kravet for at en funktion er "differentiabel" er at den er "differentiabel i alle punkter".
En funktion er differentiabel i et punkt hvis der er en kvantificerbar hældning. Du kan tænke på det som at funktionen skal ligne en (ikke lodret) linje før eller siden når der zoomes tilstrækkeligt ind på punktet.
Ingen af disse er differentiable i x=0:

Den røde er diskontinuert, resten er kontinuert men ikke differentiabel i x=0.
Når du zoomer på den gule bliver hældningen ved med at være +1 i højre side men -1 til venstre, så det flader aldrig ud til en linje.
Når du zoomer på den grønne vil det ligne en linje, men hældningen bliver større hele tiden uden at stoppe, så du ender ikke med at få et tal som kunne være hældningen.
Når du zoomer på den blå ændrer den aldrig udseende, og sekanten svinger mellem -1 og 1 inklusiv alle værdier imellem.
Svar #3
15. november 2023 af oppenede
Nej, blå/grøn/gul illustrerer kontinuitet uden differentiabilitet.
Svar #4
15. november 2023 af peter lind
Den skal også være differentiabel hvilket vil sige at i ethvert punkt x0 skal (f(x0+Δx) - f(x) )/Δx have en grænseværdi for Δx->0
Hvis den opfylder definitionen for at være differentiabel er den også kontinuert, så det er faktisk et overflødigt krav at den skal være kontinuert
Svar #5
15. november 2023 af hhxelev1
Men de vil vel alle sammen være linjer, hvis du zoomer nok ind på dem?
Svar #6
15. november 2023 af ringstedLC
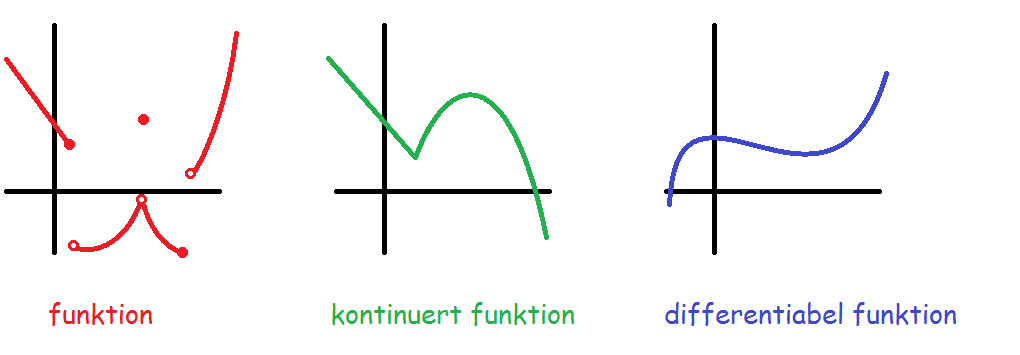
Den differentiable funktion har ingen "knæk" og er sammenhængende (kontinuert).
Skriv et svar til: Krav for differentiabel funktion
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.





