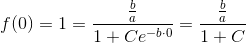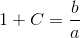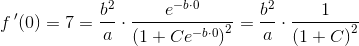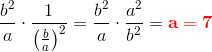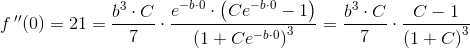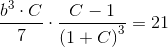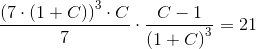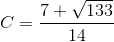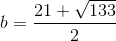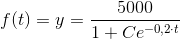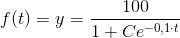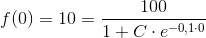Matematik

OPGAVER

31. oktober 2014 af Bitten16 (Slettet) - Niveau: B-niveau

Hjælp til opg. 358. 359. og 360. Med mellemregninger + forklaringer, tak. HASTER ..

Vedhæftet fil: IMG_2192.JPG

Brugbart svar (0)

Svar #1
31. oktober 2014 af PeterValberg

Se sidste video på denne [ VIDEO-LISTE ] fra FriViden.dk

og eventuelt video nr. 6 (talt fra oven), det er et eksempel

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #2
31. oktober 2014 af mathon

358

Løsningen til
$\frac{\mathrm{d} y}{\mathrm{d} x}=y\left ( b-ay \right )$
er
$f(x)=y=\frac{\frac{b}{a}}{1+Ce^{-bx}}$

$f{\, }'(x)=\frac{b^2}{a}\cdot \frac{e^{-bx}}{\left (1+Ce^{-bx} \right )^2}$

$f{\, }''(x)=\frac{b^3\cdot C}{a}\cdot \frac{e^{-bx}\cdot \left ( Ce^{-bx}-1 \right )}{\left (1+Ce^{-bx} \right )^3}$

Brugbart svar (0)

Svar #3
31. oktober 2014 af mathon

hvoraf
$f(0)=1=\frac{\frac{b}{a}}{1+Ce^{-b\cdot 0}}=\frac{\frac{b}{a}}{1+C}$
$1+C=\frac{b}{a}$

$f{\, }'(0)=7=\frac{b^2}{a}\cdot \frac{e^{-b\cdot 0}}{\left (1+Ce^{-b\cdot 0} \right )^2}=\frac{b^2}{a}\cdot \frac{1}{\left ( 1+C \right )^2}$

$\frac{b^2}{a}\cdot \frac{1}{\left ( \frac{b}{a} \right )^2}=\frac{b^2}{a}\cdot \frac{a^2}{b^2}={\color{Red} \mathbf{a=7}}$

$f{\, }''(0)=21=\frac{b^3\cdot C}{7}\cdot \frac{e^{-b\cdot 0}\cdot \left ( Ce^{-b\cdot 0}-1 \right )}{\left (1+Ce^{-b\cdot 0} \right )^3}=\frac{b^3\cdot C}{7}\cdot \frac{C-1}{\left ( 1+C \right )^3}$

$\frac{b^3\cdot C}{7}\cdot \frac{C-1}{\left ( 1+C \right )^3}=21$

$\frac{\left (7\cdot \left ( 1+C \right ) \right )^3\cdot C}{7}\cdot \frac{C-1}{\left ( 1+C \right )^3}=21$

$C=\frac{7+\sqrt{133}}{14}$

Brugbart svar (0)

Svar #4
31. oktober 2014 af mathon

$b=\frac{21+\sqrt{133}}{2}$

Brugbart svar (0)

Svar #5
31. oktober 2014 af mathon

359
$f(t)=y=\frac{5000}{1+Ce^{-0,2\cdot t}}$

Brugbart svar (0)

Svar #6
31. oktober 2014 af mathon

360

$f(t)=y=\frac{100}{1+Ce^{-0,1\cdot t}}$

                         $f(0)=10=\frac{100}{1+C\cdot e^{-0,1\cdot 0}}$
                                                                      1+C=10
                                                                      C=9

$f(t)=y=\frac{100}{1+9\cdot e^{-0,1\cdot t}}$

$t=10\cdot \ln\left ( \frac{9\cdot y}{100-y} \right )$

Skriv et svar til: OPGAVER

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.