Mængder

a)

Lad y være et vilkårligt element i A. Der er da to muligheder: enten tilhører y værdimængden for f, eller også gør det ikke. I det første tilfælde gælder der per definition og per antagelse at 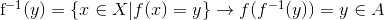. I det andet tilfælde gælder der at 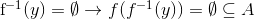da da 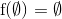. Dermed har vi vist at for et vilkårligt element  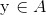gælder der at 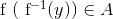, så .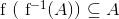

Alternativt kunne vi, hvis vi springer lidt let henover detaljerne, også have brugt nogle sætteoretiske regneregler til at skrive 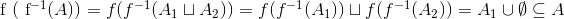, hvor  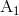er den del af A der tilhører værdimængden for f og  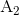er den del der ligger udenfor værdimængden.

b)

Generelt er dette ikke sandt. Ovenfor viste vi at 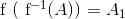, hvor 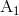er fællesmængden mellem A og værdimængden for f. Hvis  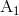derfor er strengt mindre end A gælder ligheden ikke. Hvis vi eksempelvis lader 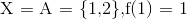og 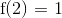har vi at 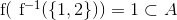. Bemærk at b) er sand hvis f er surjektiv eller A er en delmængde af værdimængden for f, for da er .

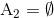c)

Generelt ikke sandt. Genbrug eksemplet fra før med 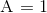. Så er .

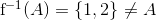- Jacob

c)

Generelt ikke sandt. Genbrug eksemplet fra før med . Så er .

I forrige eksempel var A={1,2}. Det kan da ikke bruges

Ja, det er mig der er lidt sjusket med formuleringen. Genbrug f men lad A = {1} i stedet for {1,2}

#3

Ja, det er mig der er lidt sjusket med formuleringen. Genbrug f men lad A = {1} i stedet for {1,2}

Det var det jeg tænkte :)

Men dette er da ikke et modeksempel til c) ?

f^-1(A)={1,2}≠A er rigtigt, men det er jo også tydeligt at f^-1(A)={1,2}⊄A, så betingelsen er jo ikke opfyldt?

Eller har jeg stirret mig blind på det?

Fordi udsagnen er falsk, behøver man så ikke at bekymre sig om f(A) ⊆ A og f−1(A) ⊆ A (i opgave c, stadigvæk?)

f^-1(A)=A <=> f(A)⊆A og f^-1(A)⊆A

"=>"

antag at f^-1(A)=A, da gælder f^-1(A)⊆A åbenlyst og A=f^-1(A) => f(A)=f(f^-1(A))⊆A pr. opg. 1)

"<="

Antag at f(A)⊆A og f^-1(A)⊆A.

f(A)⊆A => f^-1(f(A))⊆f^-1(A)⊆A, (det sidste pr. antagelse.

Det kan vises at A⊆f^-1(f(A)) på nogenlunde tilsvarende måde som a). altså har vi at:

A⊆f^-1(f(A))⊆f^-1(A)⊆A, eller f^-1(A)=A.

Jeg vil mene udsagnet er sandt.

Ah, jeg gik ud fra at det bare var 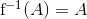der skulle modbevises. Hvis der er ækvivalensen af de to udtryk i c) der skal bevises/modbevises har jeg gjort det på præcis samme måde som i #7. Den største udfordring er så at vise at 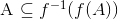er sandt, ellers er resten rimelig ligetil.

Så er jeg også enig :)