Matematik
Bestem arealet af M. Integralregning?
23. marts 2017 af
atxn (Slettet)
-
Niveau: B-niveau
 Nogen der ved hvordan man løser dette? Jeg tænker det er noget med integralregning, men ved ikke helt hvordan.
Nogen der ved hvordan man løser dette? Jeg tænker det er noget med integralregning, men ved ikke helt hvordan.
Svar #5
23. marts 2017 af atxn (Slettet)
Mange tak for hjælpen, men hvordan vidste du hvad integrationsgrænserne var?
Skriv et svar til: Bestem arealet af M. Integralregning?
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.




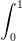
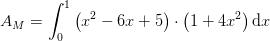
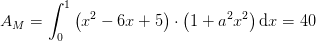
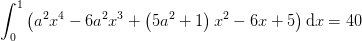
![\left [\frac{a^2}{5}x^5-\frac{3}{2}a^2x^4+\frac{5a^2+1}{3}x^3-3x^2+5x \right ]_{0}^{1}=40](https://media.studieportalen.dk/images/equations/R1IScUsdGDwJwnje5BhQzg==.gif)
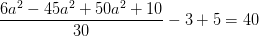
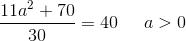
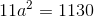
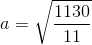
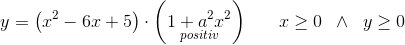
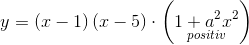 som kun giver et område afgrænset af koordinatakserne og grafen i første kvadrant for
som kun giver et område afgrænset af koordinatakserne og grafen i første kvadrant for ![x\in \left [ 0;1 \right ]](https://media.studieportalen.dk/images/equations/Z2Lhz6V-UITU66ots2h8vQ==.gif)