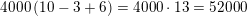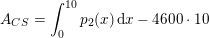Matematik
Opgaver
Svar #1
21. september 2017 af PeterValberg
a) benyt på hvert led reglen:
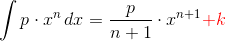
hvor k er integrationskonstanten (ved ubestemt integral)
Svar #2
21. september 2017 af StoreNord
#0 Du kan gange ind i parentesen for at gøre det lidt nemmere.
Hvis man differentierer -1/x får man netop 1/x²
Svar #4
21. september 2017 af StoreNord
Angående #2 nåh nej, du kan selvfølgelig ikke gange ind i parentesen. Den er jo i -2 . :)
Men linje 2 er rigtig nok.
Svar #5
21. september 2017 af StoreNord
#0 Betragt foreløbig kun andet led. Det er resultatet af differentiering af en sammensat funktion, hvor sen indre funktion er x-10 .
Svar #6
21. september 2017 af Mie12345678 (Slettet)
Svar #7
21. september 2017 af StoreNord
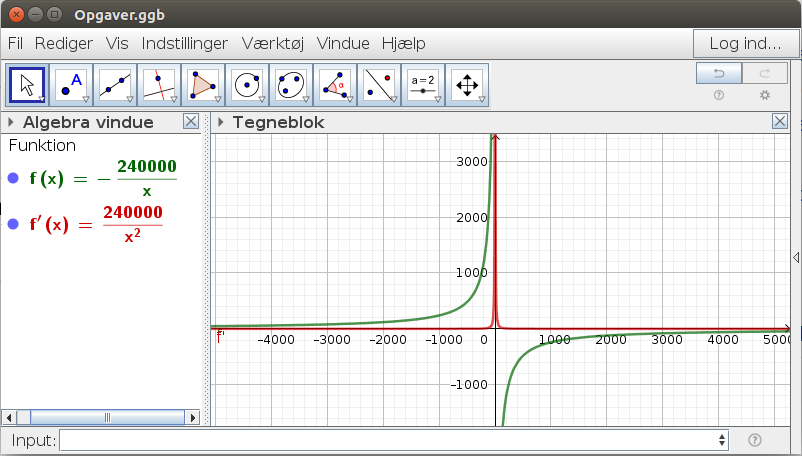
Det er jo præcis den modsatte funktion.
I vedhæftede skitse er den røde funktion 2. led i din opgave.
Det er opstået ved en differentiering af den grønne funktion.
Skriv et svar til: Opgaver
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.







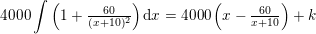
![\small 4000\int_{0}^{10} \left (1+\tfrac{60}{(x+10)^2} \right )\mathrm{d}x=4000\left [ x-\tfrac{60}{x+10} \right ]_{0}^{10}=4000\left ( 10-\tfrac{60}{20}-\left ( 0-\tfrac{60}{10} \right ) \right )=](https://media.studieportalen.dk/images/equations/KzDhnLp_PLz6iJmTi6ucUQ==.gif)