Matematik
Vektor-Gitterkonstruktion i form
hej
er det nogle det kan hjælpe lidt med den opgave?
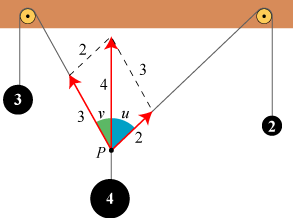
"En simpel gitterkonstruktion i form af to stænger fastgjort i terræn påvirkes af en lodret kraft på 4 kN i knudepunktet. Bestem stangkræfterne i de to stænger" 
Svar #2
05. april 2018 af DeepOcean
Og hvordan man beregn komposent vinkler
Svar #3
05. april 2018 af DeepOcean
hvad er din φ1 og hvad er φ2?? vil du være venlig og forklar lidt hvordan du kommer frem til selv formel for F1 og F2 ..??
Svar #4
05. april 2018 af Eksperimentalfysikeren
Læg mærke til, at stangen til højre er halvt så lang som afstanden mellem fastgørinspunkterne.
Kald fastgøringspunkterne A (til venstre) og B ( til højre). Knudepuktet kaldes C. Da BC er halvt så lang som AB og vinkel A er 30º, er trekant ABC retvinklet. Heraf fås, at AC er 3√3 m lang (Pythagoras). Forlænges kraftens angrebslinie ned til AB, fås punktet H. Trekant ACH og trekant CBH er begge retvinklede og ensvinklede. Tegn nu kræfterne med angrebspunkt i C. Endepunktet af den lodrette kraft kaldes K. Parallelt med AC tegnes et liniestykke fra K til punktet P, der ligger på BC og er endepunkt for den højre stangkraft. Trekant CKP er nu retvinklet og ensvinklet med ABC, hvorfor kræfterne har samme forhold som siderne i ABC.
Svar #7
05. april 2018 af DeepOcean
Mathon har du nogle ider ?
Svar #8
05. april 2018 af DeepOcean
K punkt så mister jeg tråden
Har du muligheden at sende en tegning over din løsning
Tak
Svar #9
05. april 2018 af Eksperimentalfysikeren
Det har jeg desværre ikke mulighed for, men jeg prøver på en anden måde.
Summen af to kræfter kan findes grafisk ved at man tegner et parallellogram, hvor de to kræfte repræsenteres af to nabosider. Diagonalen er så summen. I det aktuelle tilfælde bliver parallellogrammet et rektangel.
Det, der er det væsentlige, er, at vinklerne er 30º, 60º og 90º. Det giver et sideforhold på 1, √3, 2. Ved hjælp af ensvinklede trekanter kan man så finde frem til, at det samme må gælde for kræfterne.
Svar #10
05. april 2018 af Eksperimentalfysikeren
UPS: Jeg har lige opdaget en tynd streg med pilespidser ved målet 3m. Den havde jeg overset.
Målet er IKKE, som jeg troede, stanglængden, men højden af knuden over jorden.
Nedfæld den vinkelrette fra knuden på jorden. Derved fremkommer der en retvinklet trekant, hvis ene spidse vinkel er den opgivne på 30º. Hypotenusen i denne trekant er dobbelt så lang som den korteste katete, så den er 6m, hvilket er afstanden mellem de to fastgørelser. Den trekant, jeg tidligere har kaldt ABC er derfor ligebenet med A som toppunkt. Topvinklen er 30º, så der er 150º tilbage til de to andre vinkler, der er lige store, så de bliver 75º. I C deler den lodrette linie vinklen i en del, der er 60º, og en rest, der så er 15º.
Svar #11
06. april 2018 af DeepOcean
jeg har forstået hvor kommer vinkel 15 grad fra ,,men jeg forstår ikke hvordan Mathon har gjorde den i #5
jeg har brug for en skister ,for at se tingene mere klar og tydligt,,,
Trekant ABC er ensvinkel med BHC og AHC ??
Svar #12
06. april 2018 af DeepOcean
Mathon ,,har du muligheden for at sætte en tegning over din løsning med de trekanter som du har valgt ,ellers jeg kan desværre ikke følge helt med!!
Skriv et svar til: Vektor-Gitterkonstruktion i form
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.