Matematik

Differentiet

18. juli 2018 af Mie12345678 (Slettet) - Niveau: A-niveau

(3x^2-2)*(In(x^-1)+1)

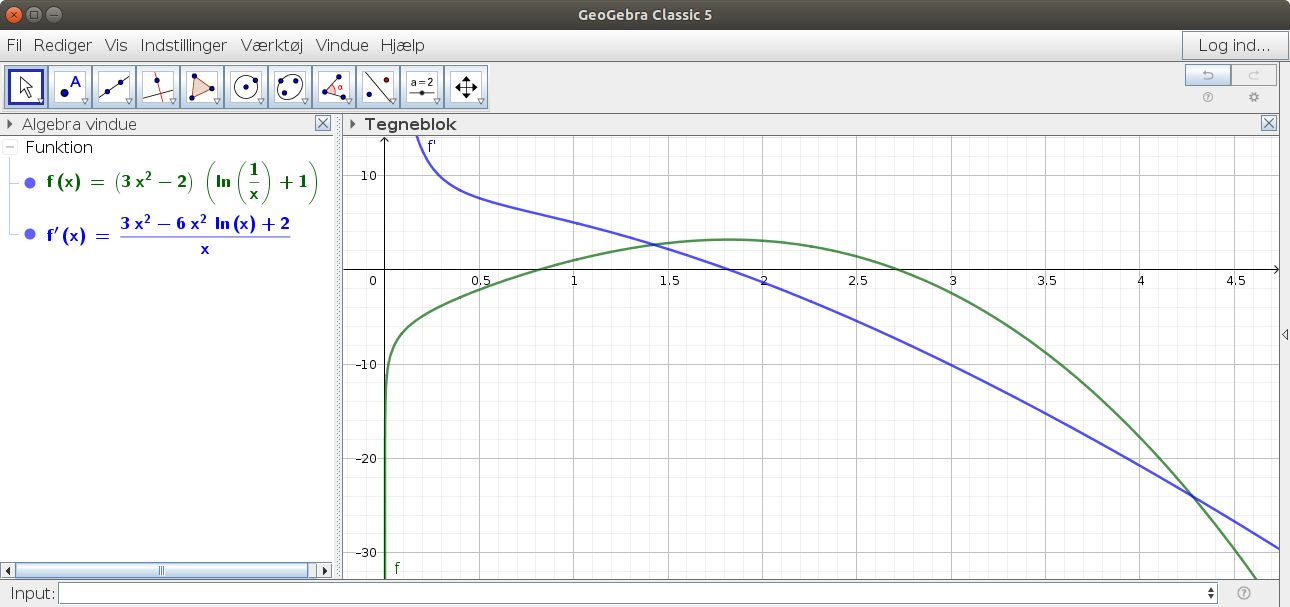
Skal man bruge produktregel, og hvordan differentierer man In(x^-1)?

Brugbart svar (0)

Svar #1
18. juli 2018 af StoreNord

Jeg ville nok gange parenteserne sammen.

In(x^-1) = ln(1/x)

Svar #2
18. juli 2018 af Mie12345678 (Slettet)

Skal man bruge kæderegel her?

Brugbart svar (0)

Svar #3
18. juli 2018 af StoreNord

Først skal du udnytte, at ln(1/x) er ln(1)-ln(x).

Når du har ganget det sammen til en flerledet størrelse, er der kun eet besværligt led.
På dette led led skal du bruge produktregel.

Brugbart svar (0)

Svar #4
18. juli 2018 af guuoo2

( (3x^2-2)*(In(x^-1)+1) )' omskriv med ln(x^a) = a·ln(x)
( (3x^2-2)*(-In(x)+1) )' brug produktreglen
(3x^2-2)' * (In(x^-1)+1) + (3x^2-2) * (-In(x)+1)' differentier polynomiet og logaritmen
6x * (In(x^-1)+1) + (3x^2-2) * (-1/x)

Svar #5
18. juli 2018 af Mie12345678 (Slettet)

Altså kan man ikke bruge kæderegel hvor man siger at f(x)=In(x) og g(x)= x^-1

1/x^-1*-x*^-2

Brugbart svar (0)

Svar #6
18. juli 2018 af mathon

$\small \left (\ln(x^{-1}) \right ){ }'=\frac{1}{x^{-1}}\cdot (-1)\cdot x^{-2}=-x^{1-2}=-x^{-1}$

$\small \small \left ((3x^2-2)\cdot \left ( \ln(x^{-1})+1 \right ) \right ){}'=6x\cdot \left ( \ln(x^{-1})+1 \right )+\left ( 3x^2-2 \right )\cdot (-x^{-1})=$

$\small 6x\cdot \left ( \ln(x^{-1})+1 \right )-\left ( 3x^2-2 \right )\cdot x^{-1}=6x\ln(x^{-1})+6x-3x+2x^{-1}=$

$\small 6x\ln(x^{-1})+3x+2x^{-1}=3x\cdot \left ( 2\ln(x^{-1})+1 \right )+2x^{-1}$

Brugbart svar (0)

Svar #7
18. juli 2018 af StoreNord

Skærmbillede fra 2018-07-18 20-04-38.png

Vedhæftet fil:Skærmbillede fra 2018-07-18 20-04-38.png

Skriv et svar til: Differentiet

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.