Matematik

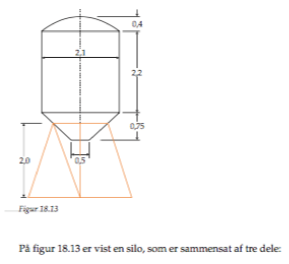
Beregn rumfanget af siloen side 704-705

07. september 2018 af OscarS - Niveau: A-niveau

Har problemer med opgaven: "Siloen" punkt a.

Jeg skal beregne rumfanget af siloen, og jeg har beregnet rumfanget af hele siloen pånær toppen (cirkelafsnittet). Hvordan gør jeg det?

Jeg har fundet formlen for beregning af rumfang for cirkelafsnit, men jeg kender jo ikke radiussen...

https://www.regneregler.dk/cirkelafsnit-areal

Håber nogen kan og vil hjælpe.

Oscar

P.s.: Tegningen af siloen er vedhæftet, og alle mål er i meter.

Vedhæftet fil: Skærmbillede 2018-09-07 kl. 12.37.47.png

Brugbart svar (0)

Svar #1
07. september 2018 af mathon

Brugbart svar (0)

Svar #2
07. september 2018 af mathon

Brug Volumenformlerne for:
$\small \small \begin{array}{lcl} \bullet\textup{ Kugleafsnit}\\ \bullet\textup{ Cylinder }\\ \bullet\textup{ Keglestub} \end{array}$

Brugbart svar (0)

Svar #3
07. september 2018 af mathon

$\small \begin{array}{lccl}& V_{kuglea\! fsnit}:&=&\frac{\pi }{3}\cdot h^2\cdot \left ( 3r-h \right )\\ \textup{hvor \textbf{h} er kugleafsnittets h\o jde}\\ \textup{og \textbf{r} er kuglens radius.} \end{array}$

Brugbart svar (0)

Svar #4
07. september 2018 af StoreNord

Du kender jo ikke radiussen, nej.

Inde i kalotten er der en kegle. Keglens tværsnit er en ligebenet trekant med alle hjørner på cirklen.
Tegn trekanten i et koordinatsystem og tegn de skrå korders midtnormaler.
De skærer hinanden i centrum.?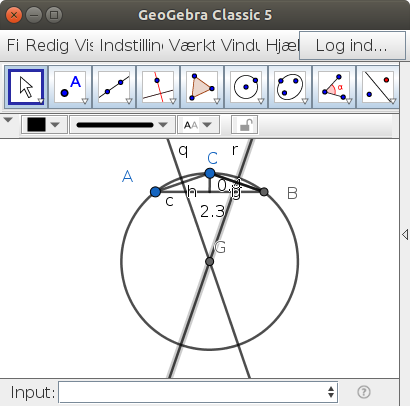

Vedhæftet fil:Kalotradius.png

Brugbart svar (0)

Svar #5
07. september 2018 af guuoo2

Du kan bestemme radius ved først at bestemme centrums koordinater:

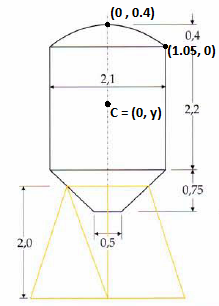
Centrum skal ligge lige langt fra de tilføjede punkter, dvs.
$\sqrt{0^2+(0.4\, -y)^2}=\sqrt{1.05^2+y^2}$

Kvadrer begge sider så det bliver til en andengradsligning med løsningen
y=-1.178125, dvs. radius er 1.578125.

Vedhæftet fil:Untitled.png

Brugbart svar (0)

Svar #6
07. september 2018 af SuneChr

En kuglekalots rumfang V_kalot kan godt bestemmes uden kendskab til kuglens radius, hvis vi kender
kalottens højde h og radius a i cirklen i afsnittet.
V_kalot = ¹/₆πh(3a² + h²)

Brugbart svar (0)

Svar #7
08. september 2018 af Eksperimentalfysikeren

Der er forskellige foslag til, hvordan man finder radius i kuglekalotten. Tegn et snit gennem kalottens symmetriakse. Tegn korden fra kant til kant. Denne korde har samme længde som diameteren, d, af cylinderdelen af siloen. Sammen med de to kugleradier danner den en ligebenet trekant. Korden skærer sykketriaksen stykket h under kuglefladen, så afstanden fra skæringspunktet til kuglecenteret er (R-h). Symmetriaksen og korden står vinkelret på hinanden, så den halve korde, og stykket R-h danner korder i en retvinklet trekant, som har hypotenusen R. Med hjælp fra Pythagoras fås:

$R^{2} = (R-h)^{2}+(\frac{d}{2})^{2}$

Her kender du h og d og kan finde R.

Brugbart svar (0)

Svar #8
08. september 2018 af mathon

$\small \textbf{SAMMENH\AE NG I VOLUMENFORMLER}$

$\small \small ...\textup{kaldes }\tfrac{k}{2}\textup{ for \textbf{r}, som er radius i afsnitscirklen og kuglens radius kaldes \textbf{R} }$
    $\small \textup{har man af:}$
   $\small R^2=(R-h)^2+r^2$
   $\small R^2=R^2-2hR+h^2+r^2$
   $\small 3hR=\tfrac{3}{2}\left (h^2+r^2 \right )$    $\small \textup{som indsat i }\tfrac{\pi }{3}h(3hR-h^2)$
$\small \textup{giver:}$
   $\small \tfrac{\pi }{3}h\left ( \tfrac{3}{2}h^2+\tfrac{3}{2}r^2-h^2 \right )$
   $\small \tfrac{\pi }{3}h\left ( \tfrac{3}{2}r^2+\tfrac{1}{2}h^2 \right )$
   $\small \tfrac{\pi }{6}h\left ( 3r^2+h^2 \right )$    $\small \textup{i overensstemmelse med }\#6.$

Brugbart svar (0)

Svar #9
08. september 2018 af StoreNord

#7 Du skriver: "Denne korde har samme længde som diameteren, d, af cylinderdelen af siloen."
Det er lodret forkert i denne opgave. Toppen er ikke en halvkugle.

Brugbart svar (0)

Svar #10
08. september 2018 af mathon

#9:
Kuglekalottens snitcirkel har da samme diameter som den underliggende cylinder,
hvis beholderen skal være tæt.

Brugbart svar (0)

Svar #11
08. september 2018 af mathon

At diameteren af den kugle, hvoraf der er snittet, er større end cylinderdiameteren er en anden sag.

Skriv et svar til: Beregn rumfanget af siloen side 704-705

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.