Matematik

Rumfang at et omdrejningslegeme

31. maj 2019 af Signekas - Niveau: A-niveau

Hej

Jeg skal gøre rede for formlen for en omdrejningslegeme i min mundtlige disposition. (Vedhæftet)

Jeg skal lave bevis i det spørgsmål også, så regner ikke med at ville bevise den for omdrejningslegemet. Men hvordan kan jeg gøre rede for formlen?

Vedhæftet fil: Skærmbillede 2019-05-31 kl. 12.52.46.png

Svar #1
31. maj 2019 af Signekas

Kan man gøre det vha. et eksempel? Hvor jeg udregner arealet at et omdrejningslegeme? Ellers er jeg på bar bund

Brugbart svar (1)

Svar #2
31. maj 2019 af Capion1

Generelt skal legemet skæres op i smalle skiver af tykkelsen Δx og radius f (x).
Rumfanget af en sådan skive er π·[f (x)]²·Δx
Ved at opsummere alle skivers rumfang i intervallet vil summen af dem ved grænseovergangen Δx → 0
være lig med integralet, som du nævnte.

Brugbart svar (0)

Svar #3
31. maj 2019 af mathon

Du formodes at arbejde med en funktion
$\small y=f(x)>0$ i hele definitionsmængden.

Fininddel x-intervallet $\small \left [ a;b \right ]$

$\small a=x_o<x_1<x_2<...<x_n=b$ så $\small x_{i+1}=x_i=\Delta x$

Ved en 360 graders drejning om x-aksen,
vil en tynd skive med radius $\small f(x_i)$ få arealet $\small \pi \cdot f(x_i)^2$ og rumfanget $\small \pi \cdot f(x_i)^2\cdot \Delta x$

Det summerede volumen bliver
da:
$\small V=\pi \cdot \int_{a}^{b}f(x)^2\mathrm{d}x$

Brugbart svar (0)

Svar #4
31. maj 2019 af ringstedLC

Et eksempel: Det var en smutter.

Vedhæftet fil:__0.png

Brugbart svar (0)

Svar #5
31. maj 2019 af ringstedLC

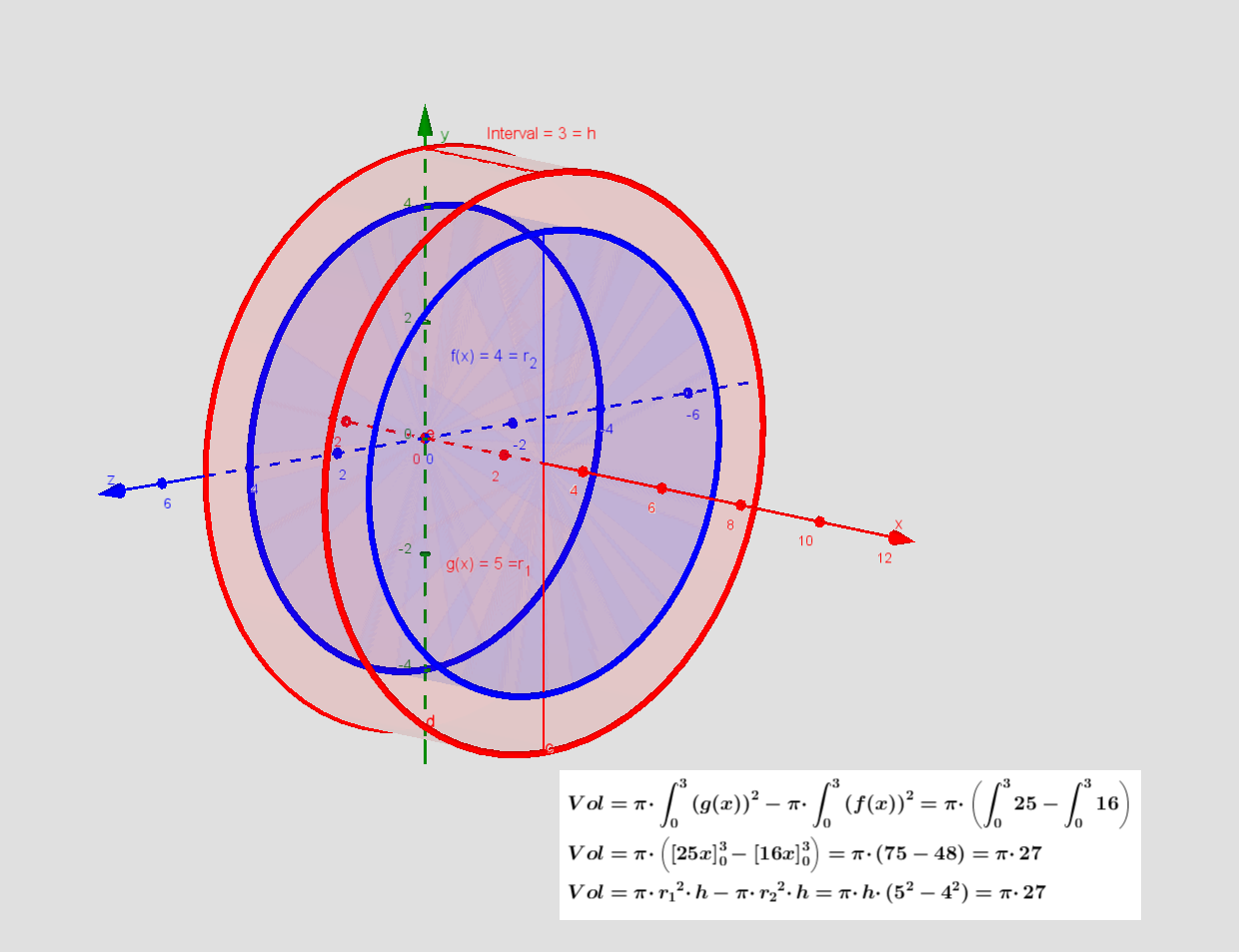
Et eksempel hvor den drejede punktmængde er afgrænset af to funktioner:

Vedhæftet fil:__0.png

Brugbart svar (0)

Svar #6
01. juni 2019 af mathon

eks. keglens volumen:

$\small \begin{array}{llll} \textup{funktion:}&f(x)=\frac{r}{h}x\\\\ \textup{volumen:}&\pi \cdot \int_{0}^{h}(\frac{r}{h}x)^2\, \mathrm{d}x\\\\ &\pi \cdot \frac{r^2}{h^2}\int_{0}^{h}x^2\, \mathrm{d}x\\\\ &\pi \cdot \frac{r^2}{h^2}\cdot \left [ \frac{1}{3}x^3 \right ]_{0}^{h}\\\\ &\pi \cdot \frac{r^2}{h^2}\cdot\frac{1}{3}\cdot h^3\\\\ &\frac{1}{3}\cdot h\cdot \pi \cdot r^2 \end{array}$

Brugbart svar (0)

Svar #7
01. juni 2019 af mathon

eks.2 kuglens volumen:

$\small \small \small \begin{array}{llll} \textup{funktion:}&f(x)=\sqrt{r^2-x^2}\\\\ \textup{volumen:}&\pi \cdot \int_{-r}^{r }(\sqrt{r^2-x^2})^2\, \mathrm{d}x\\\\ &\pi \cdot \int_{-r}^{r}r^2-x^2\, \mathrm{d}x\\\\ &\pi \cdot \left [ r^2x-\frac{1}{3}x^3 \right ]_{-r}^{r}\\\\ &\pi \cdot\left ( r^3-\frac{1}{3}r^3-\left ( -r^3-\frac{1}{3}\cdot (-r)^3 \right ) \right )\\\\ &\pi \cdot \left (2r^3-\frac{2}{3}r^3\right)\\\\ &\frac{\pi }{3}\cdot r^3 \left ( 6-2 \right )\\\\ &\frac{4 }{3}\cdot\pi\cdot r^3 \end{array}$

Brugbart svar (0)

Svar #8
13. juli 2019 af mathon

eks.3 kuglestubbens volumen:

$\small \small \begin{array}{llll} \textup{funktion:}&f(x)=\frac{R-r}{h}x+r\\\\ \textup{volumen:}&\pi \cdot \int_{0}^{h }\left(\frac{R-r}{h}x+r\right)^2\, \mathrm{d}x\\\\ &\pi \cdot \int_{0}^{h}\frac{(R-r)^2}{h^2}x^2+2\cdot \frac{(R-r)r}{h}x+r^2\, \mathrm{d}x\\\\ &\pi \cdot \left [ \frac{1}{3}\frac{\left ( R-r \right )^2}{h^2}x^3+\frac{(R-r)r}{h}x^2+r^2x \right ]_{0}^{h}\\\\& \pi \cdot \left ( \frac{1}{3}\frac{\left ( R-r \right )^2}{h^2}h^3+\frac{(R-r)r}{h}h^2+r^2h \right )\\\\&\frac{1}{3}h\pi \cdot\left ( (R-r)^2+3(R-r)r+3r^2 \right )\\\\ &\frac{1}{3}h\pi \cdot \left (R^2-2Rr+r^2+3Rr-3r^2+3r^2\right)\\\\ &\frac{1}{3}h\pi \cdot \left ( R^2+r^2+Rr \right )\end{array}$

Skriv et svar til: Rumfang at et omdrejningslegeme

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.