Matematik

Bestem nulpunkterne vha. nuplunktsreglen 2x^3(x-1)

17. juli 2019 af Warrocs - Niveau: B-niveau

Hej jeg står med en opgave hvor jeg skal bestemme nulpunkterne vha. nulpunktsreglen i en funktion med forskriften.
2x^3(x-1).

Jeg har forsøgt mig lidt frem med nogle forskellige beregninger men kan ikke få det til at give de nulpunkter som jeg har kunnet aflæse på grafen, som jeg har tegnet funktionen ind i.
Min fremgangsmåde har været:
$f(x)=2x^3-(x-1)$
Ophæv parentes
$f(x)=2x^3-x+1$
Sæt x uden for en parentes så det bliver en andensgradsligning
$f(x)=x(2x^2-1)$
Nulpunktsregel
$x(2x^2-1)=0$
$x=0\vee 2x^2-1=0$
$x=0\vee 2x^2=-1$
Isolér x
$x=0\vee x^2=-0,50$
$x=0\vee x=\sqrt{-0,5} \vee x=\sqrt{-0,5}$
Men det her giver ikke de korrekte nulpunkter, som jeg ved er 0 og 1 pågrund af grafen jeg har aflæst det på.
Er der nogen som kan sige hvor jeg fejler i min udregning?

Brugbart svar (1)

Svar #1
17. juli 2019 af Mathias7878

Hvis du har

$2x^3\cdot (x-1) = 0$

så siger nulreglen, at hvis en af faktorene er lig nul, så er x lig nul, dvs. hvis

$2x^3 = 0$

eller

$(x-1) = 0$

hvor det hurtigt ses, at

$x = 0$

eller

$x = 1$

- - -

Brugbart svar (0)

Svar #2
17. juli 2019 af mathon

$\small \begin{array}{lllllll} &f(x)=2x^3\cdot (x-1)\\\\ &2x^3\cdot (x-1)=0&\textup{kr\ae ver}\\\\ \textup{nulpunkterne}&\left \{\begin{array}{lll}\! \! 2x^3=0\Leftrightarrow x=0 \\\\ \! x-1=0\Leftrightarrow x=1 \end{array}\right. \end{array}$

Brugbart svar (0)

Svar #3
17. juli 2019 af mathon

$\small \begin{array}{llll}&\textup{N\aa r funktionen \textbf{er} i faktorer, beholdes faktorformen til bestemmelse af nulpunkterne.}\\\\ &\textup{Din foreg\aa ende opgave med bestemmelse af nulpunkter kr\ae vede forudg\aa ende faktorisering.}\\ &\textup{Dette trin udg\aa r, n\aa r funktionen \textbf{allerede er} faktoriseret.} \end{array}$

Brugbart svar (1)

Svar #4
17. juli 2019 af Eksperimentalfysikeren

Trådstarter har skrevet to forskellige funktioner: f₁(x) = 2x³*(x-1) og f₂(x) = 2x³-(x-1).Af trådstarters egne forsøg kommer jeg til det resultat, at f₁ er fremkommet ved en skrivefejl, så vi skal se på f₂.

Det første trin i #0 er korrekt, men i andet trin forsvinder konstantleddet, så resten giver et forkert resultat.

f(x) = 2x³-x+1 = x(2x²-1) +1

Da der er tale om et trediegradspolynomium, gætter jeg på, at det er valgt, så det har en heltallig løsning. Ved at prøve med x=0, x=1, x=-1 kommer jeg frem til, at x=-1 er rod i polynomiet. Denne oplysning skulle give mulighed for at komme videre.

Brugbart svar (0)

Svar #5
17. juli 2019 af oppenede

I #0 skriver du først

Men også "nulpunkter, som jeg ved er 0 og 1", som ikke hænger sammen da x=0 indsat i ovenstående forskrift ikke giver 0, men
$f(0)=2\cdot0^3-(0-1)=0-0+1=1$

Brugbart svar (0)

Svar #6
17. juli 2019 af Eksperimentalfysikeren

Til trådstarter:

Hvilken af de to funktioner er der tale om?

Svar #7
19. juli 2019 af Warrocs

#6
Til trådstarter:

Hvilken af de to funktioner er der tale om?

Der er tale om funktionen 2x^3(x-1)

Brugbart svar (0)

Svar #8
19. juli 2019 af ringstedLC

#7: og blandt andet derfor er alt det beregnede i #0 forkert. Brug #2/#3.

Du bryder flere regneregler:

Min fremgangsmåde har været:
$f(x)=2x^3-(x-1)$
Ophæv parentes
$f(x)=2x^3-x+1$
Sæt x uden for en parentes så det bliver en andensgradsligning
$f(x)=x(2x^2-1)$

$\begin{align*} f(x) &= 2x^3-x+1 \\ &= x\left ( 2x^2-1 \right )+1 \end{align*}$

Nulpunktsregel
$x(2x^2-1)=0$
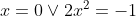
$x=0\vee 2x^2-1=0$
$x=0\vee 2x^2=-1$

$\begin{align*} 2x^2-1 &= 0 \\ 2x^2 &= 1 \end{align*}$

Isolér x
$x=0\vee x^2=-0,50$
$x=0\vee x=\sqrt{-0,5} \vee x=\sqrt{-0,5}$

$\begin{align*} x^2 &= -0.5\Rightarrow x\in \{\}\;,\;x^2\geq 0 \end{align*}$

Svar #9
21. juli 2019 af Warrocs

#8
#7: og blandt andet derfor er alt det beregnede i #0 forkert. Brug #2/#3.

Du bryder flere regneregler:

Min fremgangsmåde har været:
$f(x)=2x^3-(x-1)$
Ophæv parentes
$f(x)=2x^3-x+1$
Sæt x uden for en parentes så det bliver en andensgradsligning
$f(x)=x(2x^2-1)$

$\begin{align*} f(x) &= 2x^3-x+1 \\ &= x\left ( 2x^2-1 \right )+1 \end{align*}$

Nulpunktsregel
$x(2x^2-1)=0$
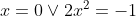
$x=0\vee 2x^2-1=0$
$x=0\vee 2x^2=-1$

$\begin{align*} 2x^2-1 &= 0 \\ 2x^2 &= 1 \end{align*}$

Isolér x
$x=0\vee x^2=-0,50$
$x=0\vee x=\sqrt{-0,5} \vee x=\sqrt{-0,5}$

$\begin{align*} x^2 &= -0.5\Rightarrow x\in \{\}\;,\;x^2\geq 0 \end{align*}$

Okay, jeg kan godt se din fremgangsmåde, og hvordan jeg skal gøre det anderledes. Men jeg forstår ikke helt dit resultat til sidst. Er resultatet ikke x= 0 eller x =1. Jeg forstår ikke hvad den sidste linje du har skrevet betyder

Brugbart svar (0)

Svar #10
21. juli 2019 af ringstedLC

Jo, jeg anviser i #8 hvordan dine udregninger skulle have været, givet at det var den stillede opgave.

Sidste linje: x tilhører den tomme mængde, da ligningen ikke har nogen løsning.

$\begin{align*} \text{Isoler x} \\ x=0&\vee x^2=-0.5\Downarrow \\ x&=0 \end{align*}$

Skriv et svar til: Bestem nulpunkterne vha. nuplunktsreglen 2x^3(x-1)

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.