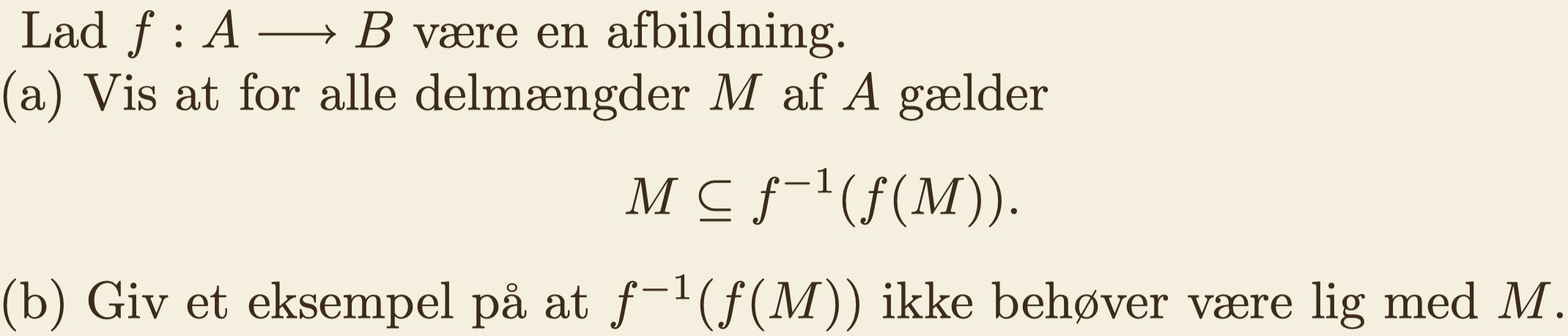Vis at for alle delmængder M af A gælder at M er en delmængde af f^(-1)(f(M))

Der er en forskel i betydningen af f^-1. Hvis du ved forstår afbildningen af elementer er det korrekt at du ikke kan tale om den inverse til f med mindre funktionen er injektiv. Der gælder så at der findes x1 og x2, x1≠x2 således at f(x1) = f(x2) Hvis du taler om f som den inverse  til billedmængden er det noget andet. Både x1 og x2 ligger i den inverse til billedmængden

eksempel  f(0) = f(1) = 2 og for x≠0∨x≠1 f(x) =3 M = {0}

f^-1(0) eksisterer ikke men f^-1(M) = {0, 1}

Man definerer for delmængder af ved

.

Bemærk at definitionen ikke kræver, at er injektiv.

Du skal vise, at hvis x ∈ M ⇒ x ∈ f^-1(f(M)).

Det svarer til at vise at f(x) ∈ f(M). Det sidste er klart sand, da x ∈ M.

#4

Du skal vise, at hvis x ∈ M ⇒ x ∈ f^-1(f(M)).

Det svarer til at vise at f(x) ∈ f(M). Det sidste er klart sand, da x ∈ M.

Okay. Tak. Nu har jeg lavet den!

b) Betragt funktionen f: R → R

Lad M = {5}. Det er let at se, at f(M) = {5}  og videre at f^-1(f(M)) = {5, 3}. Det er klart {5} ≠ {5, 3}.