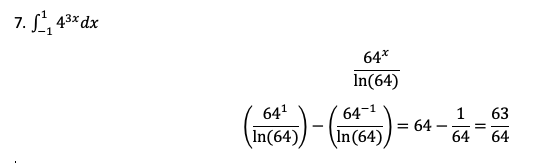Matematik

Bestemte integraler

12. november 2019 af SofieAmalieJensen - Niveau: A-niveau

Hej, jeg har fået givet følgende opgave (se vedhæftet). Jeg ville spørge om ind til opgave 7, om det kan passe at 4^3x integreret bliver (4^3x)/ln(4)?

Tak på forhånd.

Vedhæftet fil: Skærmbillede 2019-11-12 kl. 18.01.00.png

Brugbart svar (1)

Svar #1
12. november 2019 af Mathias7878

Bemærk, at

$4^{3x} = 4^{3^x} = 64^x$

dvs

$\int 4^{3x} = \frac{64^x}{ln(64)}$

eller

$\int 4^{3x} = \frac{4^{3^x}}{ln(4^3)}$

- - -

Svar #2
12. november 2019 af SofieAmalieJensen

#1
Bemærk, at

   $4^{3x} = 4^{3^x} = 64^x$

dvs

   $\int 4^{3x} = \frac{64^x}{ln(64)}$

eller

   $\int 4^{3x} = \frac{4^{3^x}}{ln(4^3)}$

Okay super mange tak:)

Svar #3
12. november 2019 af SofieAmalieJensen

#1
Bemærk, at

   $4^{3x} = 4^{3^x} = 64^x$

dvs

   $\int 4^{3x} = \frac{64^x}{ln(64)}$

eller

   $\int 4^{3x} = \frac{4^{3^x}}{ln(4^3)}$

Hvad med 8'ern? Kan det passe at det bliver (16^x)/ln(16)? Eller hvordan gælder det når der står plus mellem eksponent-ledet?

Brugbart svar (1)

Svar #4
12. november 2019 af Bibo53

#3 Det nemmeste er at benytte potensregnereglen $2^{x+4}=2^x\cdot 2^4$ . Dermed kan vi omskrive integralet til

$16\int_0^22^x\,dx$ .

Svar #5
12. november 2019 af SofieAmalieJensen

#4
#3 Det nemmeste er at benytte potensregnereglen $2^{x+4}=2^x\cdot 2^4$ . Dermed kan vi omskrive integralet til

$16\int_0^22^x\,dx$ .

Ja okay det giver god mening, så når det skal differentieres forsvinder 16, da det er en konstant?

Brugbart svar (1)

Svar #6
12. november 2019 af Bibo53

Nej, gange-konstanter skal altid blive stående. Integralet kan også skrives

$16\cdot\int_0^22^x\dx$

Du skal altså udregne

$\int_0^22^x\dx$

og så gange det med 16.

Brugbart svar (0)

Svar #7
12. november 2019 af mathon

Brugbart svar (1)

Svar #8
12. november 2019 af mathon

$\small \begin{array}{llll} 2.&\int_{-2}^{5}(2x-3)\mathrm{d}x=\left [ x^2-3x \right ]_{-2}^{5}= 5^2-3\cdot 5-( (-2)^2-3\cdot (-2))=10-(4+6)=0 \end{array}$

Brugbart svar (1)

Svar #9
12. november 2019 af mathon

$\small \small \begin{array}{llll} 3.&\int_{0}^{1}(x^2+3)\mathrm{d}x=\left [ \frac{1}{3}x^3+3x \right ]_{0}^{1}=\frac{1}{3}\cdot 1^3+3\cdot 1-0=\frac{10}{3} \end{array}$

Brugbart svar (1)

Svar #10
12. november 2019 af mathon

$\small \small \small \begin{array}{llll} 4.&\int_{0}^{\pi }\sin(x)\mathrm{d}x=\left [ -\cos(x)\right ]_{0}^{\pi }=-\cos(\pi )-(-\cos(0))=-(-1)-(-1)=2 \end{array}$

Brugbart svar (1)

Svar #11
12. november 2019 af mathon

$\small \begin{array}{llll} 7.&&\int_{-1}^{1 }4^{3x}\mathrm{d}x\\\\ &\textup{her s\ae ttes:}&u=3x\quad \textup{og dermed}\quad \frac{1}{3}\mathrm{d}u=\mathrm{d}x\quad \textup{og }\; \begin{matrix} 1\\ -1 \end{matrix}\rightarrow \begin{matrix} 3\\-3 \end{matrix}\\\\ &\textup{hvoraf:}&\int_{-1}^{1 }4^{3x}\mathrm{d}x=\frac{1}{3}\cdot \int_{-3}^{3}4^u\mathrm{d}u=\frac{1}{3}\cdot \left [ \frac{1}{\ln(4)}\cdot 4^u \right ]_{-3}^{3}=\\\\ &&\frac{1}{3\cdot \ln(4)}\cdot \left ( 4^3-4^{-3} \right )=\frac{1}{3\cdot \ln(4)}\cdot\frac{4095}{64}=\frac{1365}{64\ln(4)}=\frac{1365}{128\cdot \ln(2)} \end{array}$

Svar #12
12. november 2019 af SofieAmalieJensen

#11
$\small \begin{array}{llll} 7.&&\int_{-1}^{1 }4^{3x}\mathrm{d}x\\\\ &\textup{her s\ae ttes:}&u=3x\quad \textup{og dermed}\quad \frac{1}{3}\mathrm{d}u=\mathrm{d}x\quad \textup{og }\; \begin{matrix} 1\\ -1 \end{matrix}\rightarrow \begin{matrix} 3\\-3 \end{matrix}\\\\ &\textup{hvoraf:}&\int_{-1}^{1 }4^{3x}\mathrm{d}x=\frac{1}{3}\cdot \int_{-3}^{3}4^u\mathrm{d}u=\frac{1}{3}\cdot \left [ \frac{1}{\ln(4)}\cdot 4^u \right ]_{-3}^{3}=\\\\ &&\frac{1}{3\cdot \ln(4)}\cdot \left ( 4^3-4^{-3} \right )=\frac{1}{3\cdot \ln(4)}\cdot\frac{4095}{64}=\frac{1365}{64\ln(4)}=\frac{1365}{128\cdot \ln(2)} \end{array}$

Tak, jeg har fået det samme i dem du har sat ind, men er det forkert at lave 7'ern således, se vedhæftet.

Vedhæftet fil:Skærmbillede 2019-11-12 kl. 21.59.05.png

Brugbart svar (0)

Svar #13
13. november 2019 af mathon

Brugbart svar (1)

Svar #14
13. november 2019 af mathon

$\small \begin{array}{lllll} \int_{-1}^{1}64^x\, \mathrm{d}x=\left [\frac{1}{\ln(64)}\cdot 64^x \right ]_{-1}^{1}=\frac{1}{6\ln(2)}\cdot \left ( 64-64^{-1} \right )=\frac{1}{6\ln(2)}\cdot \frac{4095}{64}=\frac{1}{2\ln(2)}\cdot \frac{1365}{64}=\frac{1365}{128\ln(2)} \end{array}$

Skriv et svar til: Bestemte integraler

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.