Matematik

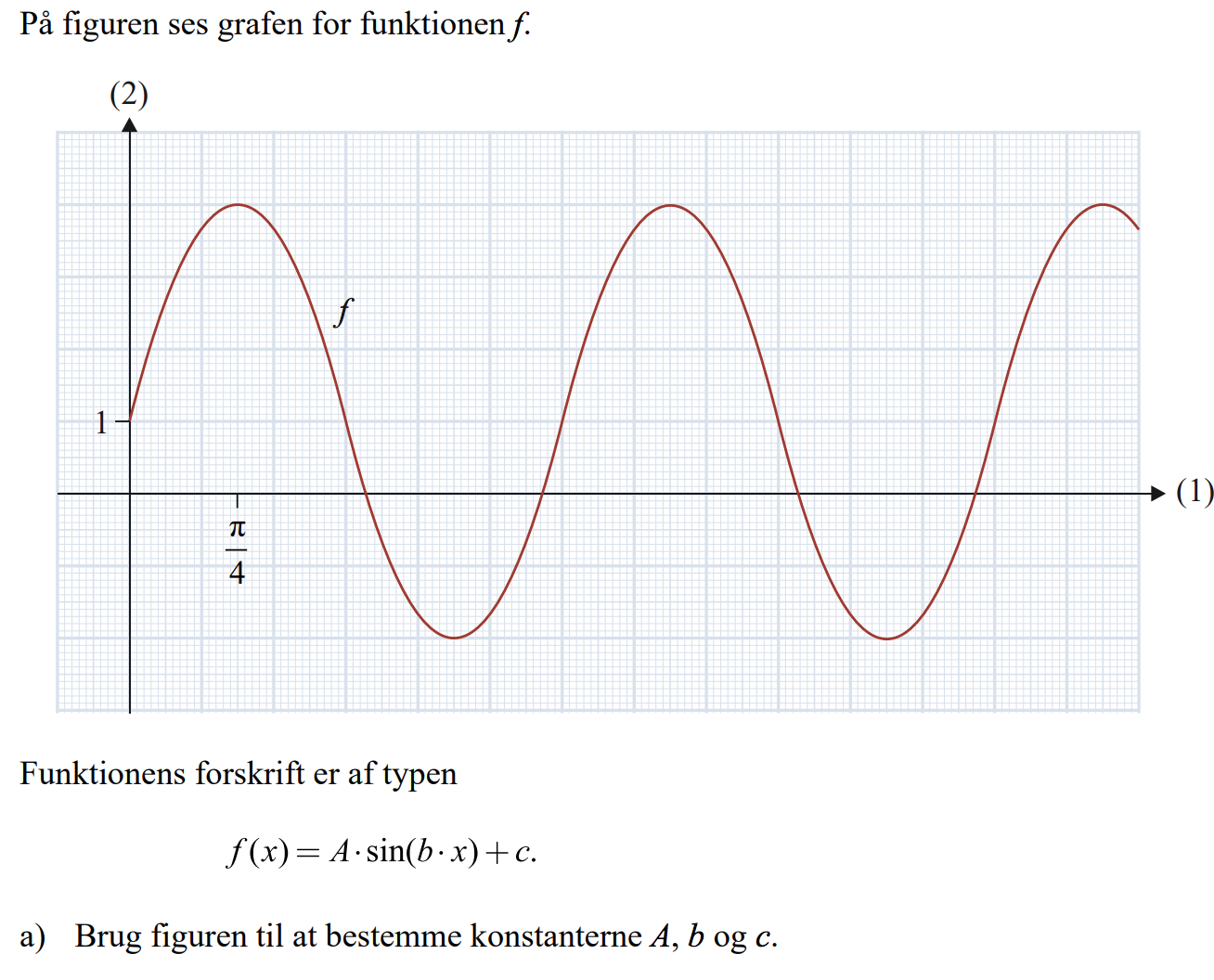
Bestem konstanterne a,b og c

18. januar 2020 af Mie23234 - Niveau: A-niveau

Nogle der kan hjælpe?

Vedhæftet fil: Skærmbillede 2020-01-18 kl. 12.43.23.png

Brugbart svar (0)

Svar #1
18. januar 2020 af mathon

Brugbart svar (0)

Svar #2
18. januar 2020 af mathon

$\small \begin{array}{llllll}f(x)=3\cdot \sin(2\cdot x)+1 \end{array}$

Svar #3
18. januar 2020 af Mie23234

#2
$\small \begin{array}{llllll}f(x)=3\cdot \sin(2\cdot x)+1 \end{array}$

Hvordan fandt du dem? Selvom du har fundet konstanterne kan jeg stadig ikke se hvordan...

Brugbart svar (0)

Svar #4
18. januar 2020 af ringstedLC

$\begin{align*} c &= \frac{f_{maks}-f_{min}}{2}=1 \\ A &= f_{maks}-c=3 \\ b &= \frac{\text{sin}_{periode}}{f_{periode}}=\frac{\text{sin}_{periode}}{4\cdot \frac{\pi}{4}}=2 \end{align*}$

Brugbart svar (0)

Svar #5
18. januar 2020 af mathon

$\small \begin{array}{lllll}f(x):=a\cdot \sin(b\cdot x)+c\quad x\in\left [ 0;\pi \right ]\\\\ \textup{solve}\left ( \left\{\begin{array}{llll}1=f(0)\\4=f\left ( \frac{\pi }{4} \right ),&\left \{ a,b,c \right \}\\-2=f\left ( \frac{3\pi }{4} \right ) \end{array}\right. \right ) \end{array}$

Svar #6
18. januar 2020 af Mie23234

#4
$\begin{align*} c &= \frac{f_{maks}-f_{min}}{2}=1 \\ A &= f_{maks}-c=3 \\ b &= \frac{\text{sin}_{periode}}{f_{periode}}=\frac{\text{sin}_{periode}}{4\cdot \frac{\pi}{4}}=2 \end{align*}$

Hvor kan man finde de formler?

Svar #7
18. januar 2020 af Mie23234

#5
$\small \begin{array}{lllll}f(x):=a\cdot \sin(b\cdot x)+c\quad x\in\left [ 0;\pi \right ]\\\\ \textup{solve}\left ( \left\{\begin{array}{llll}1=f(0)\\4=f\left ( \frac{\pi }{4} \right ),&\left \{ a,b,c \right \}\\-2=f\left ( \frac{3\pi }{4} \right ) \end{array}\right. \right ) \end{array}$

Opgaven er uden hjælpemidler...

Brugbart svar (0)

Svar #8
18. januar 2020 af ringstedLC

#6: Dem skal man på dit niveau selv kunne danne:

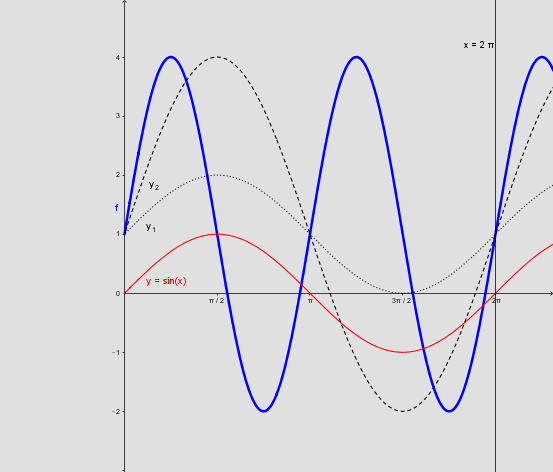
$\begin{align*} y &= \sin(x)\Rightarrow \left\{\begin{matrix} y_{maks} =1\\y_{min}=-1 \end{matrix}\right. \\ y_1 &= \sin(x)+c\Rightarrow \left\{\begin{matrix} y_{1\,maks}=1+c\\ y_{1\,min}=-1+c \end{matrix}\right. \\ y_2 &= A\cdot \sin(x)+c\Rightarrow \left\{\begin{matrix} y_{2\,maks}=A+c\\ y_{2\,min}=-A+c \end{matrix}\right. \\ &\left.\begin{matrix} f_{periode}=0.5\cdot y_{2\,periode}\\f_{frekvens}=2\cdot y_{2\,frekvens} \end{matrix}\right\}\Rightarrow b=2 \end{align*}$

Vedhæftet fil:__0.png

Skriv et svar til: Bestem konstanterne a,b og c

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.