Løs ligning f(x)=2 uden en f(x)

#1

Tegn en vandret linje ved x = 2 og aflæs den tilhørende y-værdi for at løse f(x) = 2. For at løse uligheden f(x) > 0 skal du blot se på det område, hvor y = f(x) er positiv. 

Så i denne opgave er ligningen

0=2?

Tror ikke helt jeg lige forstår hvad du mener med uligheden. For der er jo ikke særlig meget af grafen som er positiv?

Ja for at løse f(x) = 2, skal man tegne en vandret linje ved x = 2. Så bemærker man, som du rigtigt skriver, at x = 0 er en løsning til f(x) = 2. Man kan ikke skrive at  0 = 2, fordi det er jo ikke rigtigt. 

For at løse uligheden f(x) > 0, skal du finde de x-værdier, hvor f(x) er positiv, dvs. hvor grafen (den røde strege) er over x-aksen. Det er altså ikke blot et tal længere, men et interval x skal ligge i for at opfylde uligheden. 

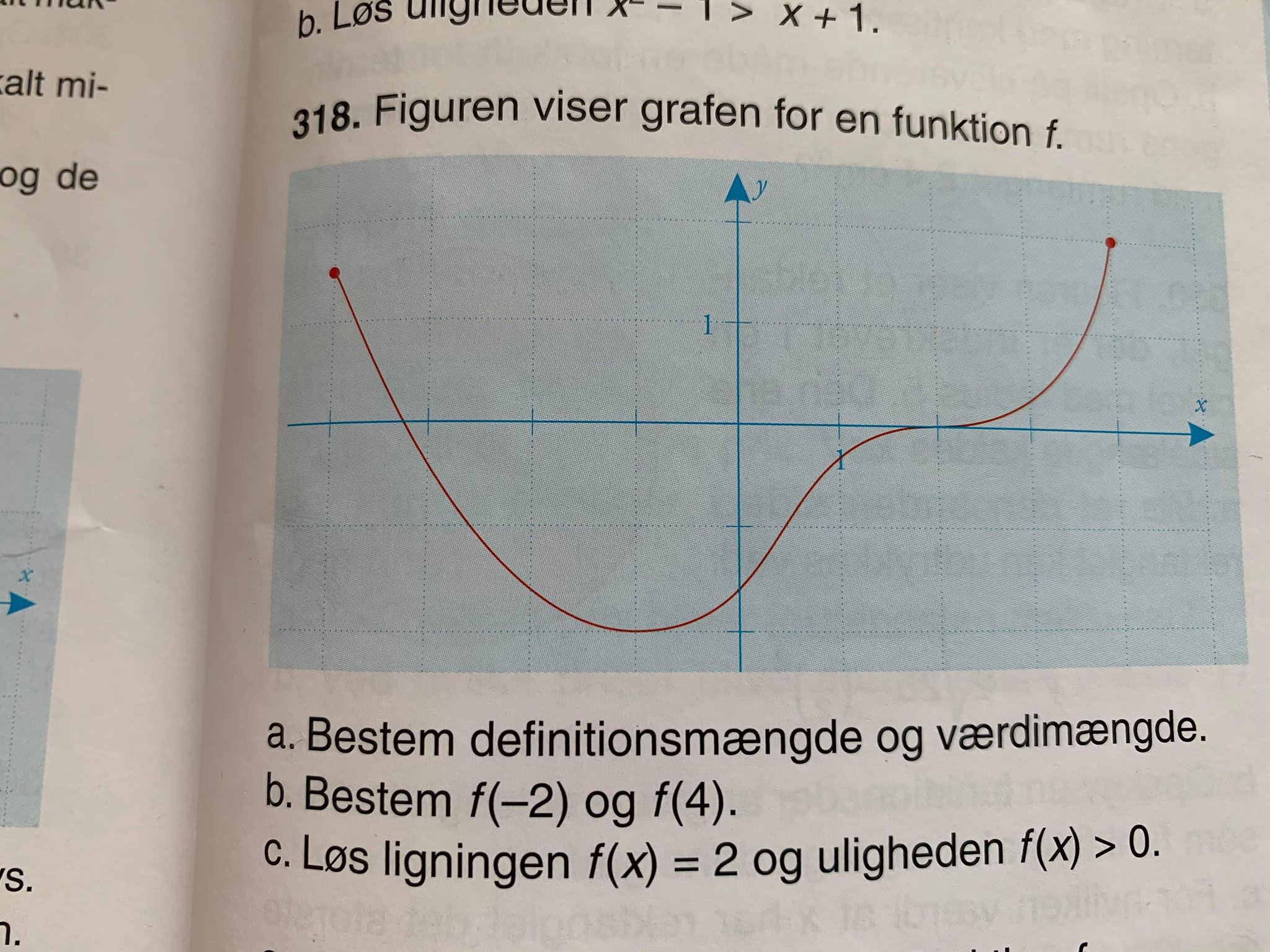
#2 og #4: Tegn en linje med ligningen y = 2 og aflæs x-værdien af dens skæring med grafen for f.

Når ja, hov. Jeg lavede vist en fejl der. 

Skrivefejl i #2 Der skulle stå vandret linje ved y = 2.

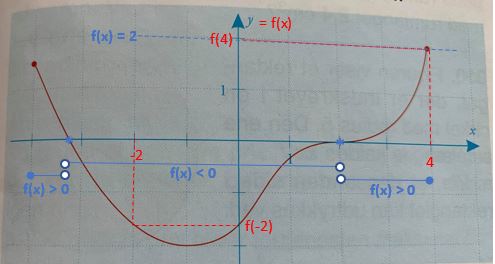
Så skal du derudfra svare på de enkelte spørgsmål.

Okay tusinde tak. Tror jeg nogenlunde har forstået det. Så lige for at være helt sikker så er f(2)=4 og uligheden er i intervallerne [-4;-3,2[ f(x) > 0 og ]-3,2;2[ f(x)<0 og ]2;4] f(x)>0.

Nej f(4) = 2 (x-værdien står inde i parentesen og f(...) er den tilsvarende y-værdi).

Du skulle løse uligheden f(x) > 0, så løsningen er L = [-4;-3,2[ ∪ ]2;4] eller skrevet på en anden måde
f(x) > 0 ⇔ -4 ≤ x < -3.2 eller 2 < x ≤ 4.

Mon ikke du mener  [-4; -3.2[  ?

#11: Selvfølgelig; - rettelse #10: