Matematik
Mindste afstand-optimering
Hej Alle
Jeg har følgende opgave håber at nogle vil hjælpe mi gmed:
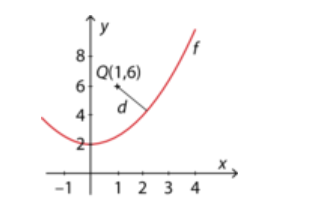
" Grafen for en funktion f med forskriften f(x) = 0.5 x^2 +2 .Der er også vist et punkt Q med koordinaterne Q(1,6). Bestem den mindste afstand d mellem Q og grafen for f.?
Figuren vedhæftes
Tak på forhånd.
Svar #2
16. juni 2020 af AMelev
Afstanden fra Q til grafpunktet P(x,f(x)) er mindst, netop når kvadratafstanden er mindst.
Beregn d(x) = PQ2 og bestem minimum for d(x) på sædvanlig vis.
Når du har fundet max for d(x), skal du huske, at det er kvadratet på den søgte afstand, du har fundet.
Svar #3
16. juni 2020 af janhaa
P = (x, 0,5x2+2) => Q = (1,6)
|PQ| = sqrt((1-x)2 + (4-0,5x2)2 ) = sqrt(1-2x+x2 +16 - 4x2 +0,25x4) = d(x)
d ' (x) = 1/(2*sqrt(...)) * (-2+2x-8x+x3) = 0
x3 - 6x - 2 = 0
Svar #4
16. juni 2020 af peter lind
kvadratet på afstanden fra Q til et punkt på kurven er (x-1)2 + (6 - ( 0.5 x2 +2)2 Minimer denne funtkion
Svar #5
16. juni 2020 af DeepOcean
når jeg løse følgende ligning x3 -6x-2 = 0 får jeg komplix tal hvad skal vi gøre?
Svar #6
16. juni 2020 af peter lind
Der er altså også en reel rod. Hvad har du gjort ? Brug dit CAS værktøj
Svar #7
16. juni 2020 af DeepOcean
#6 ja rigtigt
Efter jeg har løst ligning x3 -6x-2 = 0 får jeg 3 værdier af x nemlige -2.261 og -0.339 og 2.60 hvor jeg har fundet ud af når x = -2.26 så har afstandformel minimum værdie så skal jeg sætter den fundet x (-2.261) i selv afstandformel (PQ)2 = ( 0.25x4 -3x2 2x+1) så får jeg negative tal og jeg kan ikke kvardret negative tal ? laver jeg en fejl ?
Svar #8
16. juni 2020 af peter lind
Ja, Løsningerne gælder kun for positive værdier da en længde i kan være negativ
Svar #9
16. juni 2020 af AMelev
#7
Efter jeg har løst ligning x3 -6x-2 = 0 får jeg 3 værdier af x nemlige -2.261 og -0.339 og 2.60 Korrekt
hvor jeg har fundet ud af når x = -2.26 så har afstandformel minimum værdie
Det er ikke korrekt - prøv at tegne grafen for d(x)
så skal jeg sætter den fundet x (-2.261) i selv afstandformel (PQ)2 = ( 0.25x4 -3x2 2x+1).
Hvor får du det fra?
så får jeg negative tal og jeg kan ikke kvardret negative tal ? laver jeg en fejl ?
Ja, da det er en sum af kvadrattal, kan det ikke være negativt, men da du ikke har vedhæftet dine beregninger, kan vi ikke se, hvor du har lavet fejlen.
Skriv et svar til: Mindste afstand-optimering
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.





