Matematik

Løsning af andengradsligning hvor k er ubekendt

24. oktober 2020 af Audioholic - Niveau: B-niveau

Hejsa derude.

a) Løs ligningen f(x)=g(x) for f(x)=2x^2-4x-4 og f(x)=4x-10.

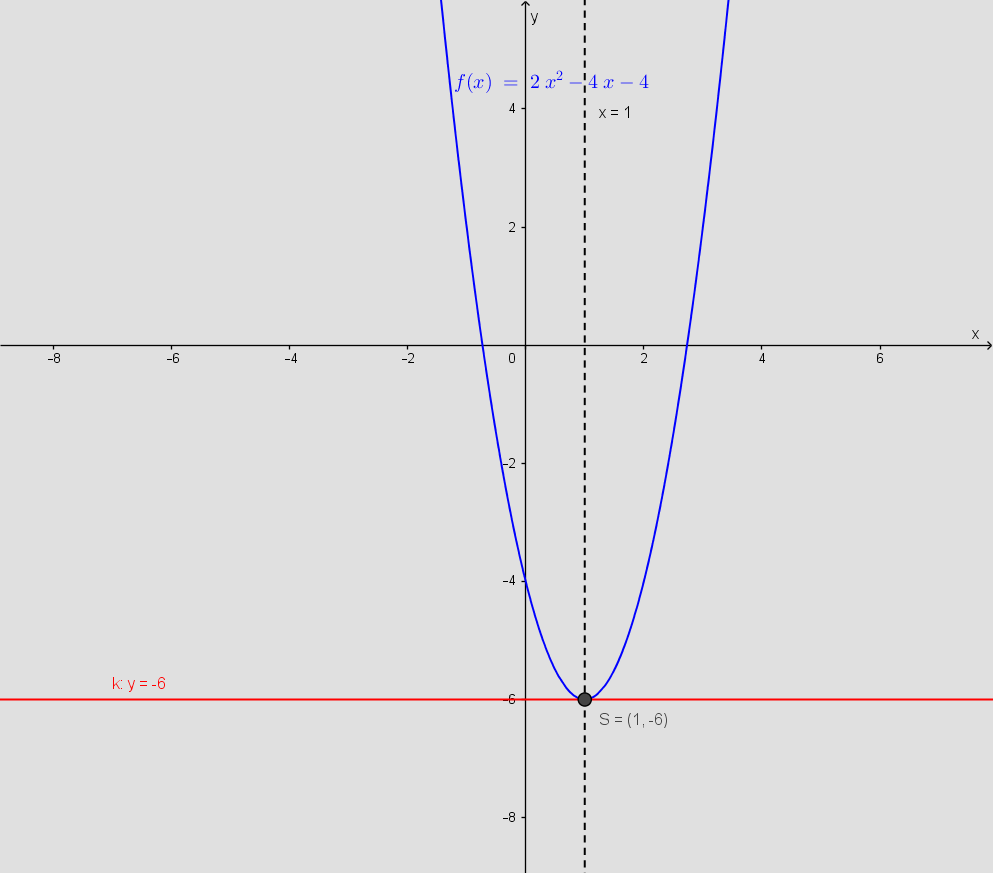
b) Bestem k så ligningen 2x^2-4x-4=k netop har én løsning.

Jeg har store problemer med at komme i gang med ovenstående opgave; Når jeg løser ligningen 2x^2-4x-4=4x-10 vha. CAS-værktøj får jeg x=1 v x=3 og på faktoriseret form er det jo f(x)=2*(x-1)(x-3) men jeg ved slet ikke, om det er sådan jeg skal gøre, og hvordan jeg kommer videre.

På forhånd tak!

Brugbart svar (0)

Svar #1
24. oktober 2020 af peter lind

a) det er sådan du skal gøre eller du skal løse den manuelt

b) determinanten af ligningen skal være 0 for at der kun er en løsning

Brugbart svar (1)

Svar #2
24. oktober 2020 af ringstedLC

a) Korrekt. Prøv at tegne de to funktioners grafer og se, at du har bestemt deres skæringers x-koordinater.

b) Grafen af venstresiden giver en glad parabel og højresiden er retlinje parallel med x-aksen. Brug din viden om diskriminanten:

$\begin{align*} 2x^2-4x-4 &= k \\ 2x^2-4x-4-k &= 0 \\ d &= b^2-4ac \\ d=\;? &= (-4)^2-4\cdot 2\cdot (-4-k)\Rightarrow 1\,\text{l\o sning} \end{align*}$

Svar #3
24. oktober 2020 af Audioholic

#2 (Ringsted LC) Jeg ved godt, at du formodentligt ikke er meget for bare at give svaret væk, men personligt, så lærer jeg meget mere af, at du viser mig hvordan man gør først. Tak! :)

Brugbart svar (1)

Svar #4
24. oktober 2020 af ringstedLC

#3: Formoder, at det må være til b):

$\begin{align*} \left.\begin{matrix} d>0&\Rightarrow& 2&\!\text{l\o sninger} \\ d=0&\Rightarrow& 1&\!\text{l\o sning} \\ d<0&\Rightarrow& 0&\!\text{l\o sninger} \end{matrix}\right\}\Rightarrow d=0 &= (-4)^2-4\cdot 2\cdot (-4-k) \\ 0 &= 16+32+8k \\ 0 &= 2+4+k \\k &= -6 \\ f(x) &= k \\ 2x^2-4x-4 &= -6 \\ 2x^2-4x+2 &=0 \\ x &= \frac{-(-4)\pm\sqrt{(-4)^2-4\cdot 2\cdot 2}}{2\cdot 2} \\ x &= \frac{4\pm 0}{4} \\ x &= 1 \end{align*}$

Vedhæftet fil:__0.png

Svar #5
24. oktober 2020 af Audioholic

Ja, det var rigtigt antaget; det var b'eren der forvoldede problemer. Mange tak for hjælpen!

Skriv et svar til: Løsning af andengradsligning hvor k er ubekendt

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.