Matematik

Hvilken funktion er det

29. november 2020 af UCL (Slettet) - Niveau: B-niveau

Funktionen f er bestemt ved f(x)=6·√x-2x

Har jeg tegnet grafen korrekt i geogebra?

Brugbart svar (1)

Svar #1
29. november 2020 af StoreNord

Det kan vi jo ikke vide.

Vedhæftet fil:Skærmbillede fra 2020-11-29 22-07-43.png

Brugbart svar (0)

Svar #2
29. november 2020 af CecilieBebsi (Slettet)

Er kvadratroden om x-2x eller kun x?
Hvis den er om x-2x er det en potensfunktion

Svar #3
29. november 2020 af UCL (Slettet)

Jeg har fået lavet samme graf som jeg skulle til et oploade som som et billede - da den ikke kunne accepterer den som fil. Jeg har fået præcis samme graf. Hvis jeg skal nu får som opgave at jeg skal løse ligningen : f’(x) = 0 skal jeg så forsøge at regne a og b ud for at komme frem til hældningskoefficienten?

Brugbart svar (0)

Svar #4
29. november 2020 af CecilieBebsi (Slettet)

F'(x)=0
Der differentierer du din funktion.
Dernæst
[differentierede funktion] = 0
Isolér x.

Svar #5
29. november 2020 af UCL (Slettet)

# 2

kvadratroden af x-2x . Hvordan er det man kan se det er en potensfunktion udefra det

Svar #6
29. november 2020 af UCL (Slettet)

# 4. Tak vil det sige jeg skal finde x og y koordinaterne og komme frem til hældningskoefficienten af grafen

Brugbart svar (2)

Svar #7
29. november 2020 af StoreNord

f(x) = 6sqrt(x) - 2x er en differens af to potensfunktioner, da den også kan skrives som
$f(x) = 6*x^{0.5} - 2*x^{1}$

Svar #8
29. november 2020 af UCL (Slettet)

Okay hvordan kan jeg differentierer min funktion: f'(x) = 0. Skal jeg finde hældningskoefficienten?

jeg har lidt svært ved at aflæse x og y koordinaterne ...

Brugbart svar (0)

Svar #9
29. november 2020 af CecilieBebsi (Slettet)

Din y-værdi for den afledede funktion er jo 0 når f'(x)=0
y=f(x)
y'=f'(x)

Så y'=0
Nu mangler du bare x-værdien som du får når du isolerer x eller vha et matematikprogram.
De x-værdier du får, er de x-værdier til punkterne (på grafen for f(x)) hvor tangenten er vandret. Hvad er hældningen når tangent er vandret?

Brugbart svar (0)

Svar #10
29. november 2020 af CecilieBebsi (Slettet)

Eller lidt mere præcist:
Nu mangler du bare x-værdien som du får når du isolerer x eller vha et matematikprogram.
De x-værdier du får, er de x-værdier hvor f'(x) skærer x-aksen. Når f'(x) skærer x-aksen, er x-værdierne på grafen for f(x), x-koordinaterne for de punkter, hvor tangenten er vandret. Hvad er tangentens hældning når den er vandret?

Svar #11
29. november 2020 af UCL (Slettet)

Altså jeg er bare gået i stå og prøver at læse om det . Det eneste jeg kan se er at grafen måske skærer x-aksen i punktet 8-10.

Brugbart svar (1)

Svar #12
29. november 2020 af StoreNord

Vedhæftet fil:Skærmbillede fra 2020-11-29 23-22-22.png

Svar #13
29. november 2020 af UCL (Slettet)

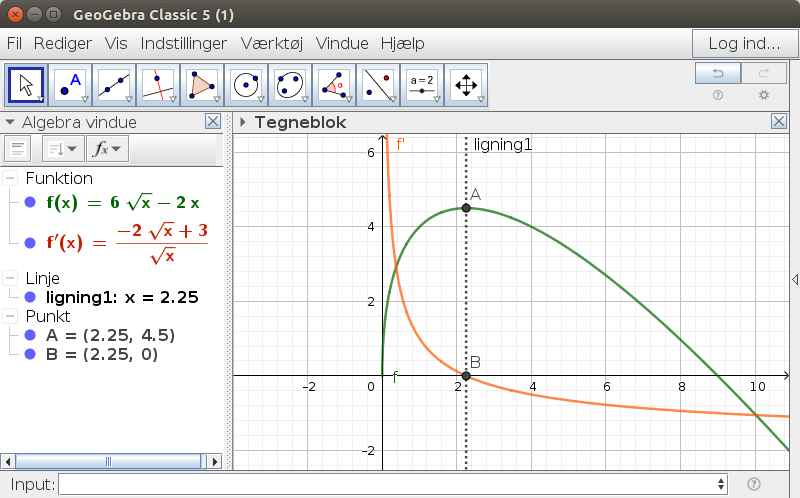
Mange mange tak #12. Men jeg fatter ikke rigtig hvad A og B? er det punkterne ,

hvordan ved du at det er der...er det toppunktet man skal kigge på så? kan du evt fortælle mig hvordan man skal tegne det ind i geogebra

Brugbart svar (0)

Svar #14
30. november 2020 af StoreNord

f'(x) er 0, hvor der er ekstremum.

I Geogebra skriver men blot f', så blir den differentieret.
Man kan også bare skrive Ekstremum(f), så får man punktet.
Den lodrette stiplede linje fik jeg ved at skrive: x=x(A)

Svar #15
30. november 2020 af UCL (Slettet)

Okay altså når jeg skriver f' så kommer der bare til at stå et spørgsmålstegn

Skriver jeg Ekstremum f, kommer der til at stå: g(x) = (6·1√x-2x )

Brugbart svar (0)

Svar #16
30. november 2020 af StoreNord

Selvfølgelig skal du først have en f, før du kan få en f'.

Ekstremum(f) husk parentesen.

Svar #17
30. november 2020 af UCL (Slettet)

Tak men jeg har skrevet det med parentes . Esktremum (f). Jeg får desværre ikke det der er vist i svar 12

Brugbart svar (0)

Svar #18
30. november 2020 af StoreNord

Der skal ikke være mellemrum.

f(x) = 6sqrt(x) - 2x

ekstremum(f)

Svar #19
30. november 2020 af UCL (Slettet)

Den siger bare det er ukendt. Jeg ved ikke hvad der går galt og hvorfor jeg ikke kan få det der er skrevet f'(x) jeg har ligningen op f(x)

Svar #20
30. november 2020 af UCL (Slettet)

Du får f' ved at skrive:ekstremum(f)?

Forrige 1 2 Næste

Der er 34 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.