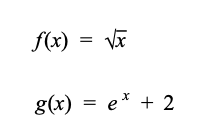Matematik

bestem differentialkvotienten

28. februar 2021 af inneedoflektiehjælp (Slettet) - Niveau: A-niveau

Hej. Jeg har disse to funktioner (vedhæftet). Jeg har bestemt f'(x) og g'(x). Er der nogen, der kan vise hvordan jeg kan bestemme differentialkvotienten af $f(x)\cdot g(x)$ ?

Brugbart svar (0)

Svar #1
28. februar 2021 af mathon

$\small \left (f(x)\cdot g(x) \right ){}'=f{\, }'(x)\cdot g(x)+f(x)\cdot g{\, }'(x)$

Svar #2
28. februar 2021 af inneedoflektiehjælp (Slettet)

men f'(x) giver 1 / 2√x? skal det indsættes ind i formlen?

Svar #3
28. februar 2021 af inneedoflektiehjælp (Slettet)

og g'(x) får jeg til e^x + 2, skal det så også bare indsættes eller...?

Brugbart svar (0)

Svar #4
28. februar 2021 af mathon

Ja.

Brugbart svar (0)

Svar #5
28. februar 2021 af AMelev

#0 Der er ikke noget vedhæftet.

Svar #6
28. februar 2021 af inneedoflektiehjælp (Slettet)

Hov. Her er det:

Vedhæftet fil:Skærmbillede 2021-02-28 kl. 15.47.58.png

Brugbart svar (0)

Svar #7
28. februar 2021 af mathon

Brugbart svar (0)

Svar #8
28. februar 2021 af mathon

$\small \begin{array}{llllll} f{\, }'(x)=\frac{1}{2\sqrt{x}}\\\\ g{\, }'(x)=e^x\\\\\\ \left (f(x)\cdot g(x)\right ) { }' =f{\, }'(x)\cdot g(x) +f(x)\cdot g{\, }'(x)=\frac{1}{2\sqrt{x}}\cdot (e^x+2)+\sqrt{x}\cdot e^x \end{array}$

Brugbart svar (1)

Svar #9
28. februar 2021 af AMelev

Væn dig til at bruge din formelsamling.
Det er også en god idé at bruge dit CAS-værktøj til tjek.

Svar #10
01. marts 2021 af inneedoflektiehjælp (Slettet)

#8
$\small \begin{array}{llllll} f{\, }'(x)=\frac{1}{2\sqrt{x}}\\\\ g{\, }'(x)=e^x\\\\\\ \left (f(x)\cdot g(x)\right ) { }' =f{\, }'(x)\cdot g(x) +f(x)\cdot g{\, }'(x)=\frac{1}{2\sqrt{x}}\cdot (e^x+2)+\sqrt{x}\cdot e^x \end{array}$

Er differentialkvotienten det som står til sidst bag lighedstegnet? Eller er der noget mere efter det, som skal regnes? Bare så jeg er sikker på, at jeg har forstået det rigtigt...

Brugbart svar (1)

Svar #11
01. marts 2021 af ringstedLC

#10: Ja. Differentialkvotienten til en funktion skal ikke give en værdi, men er en forskrift, der beskriver hældningen af funktionen for en x-værdi. Når en x-værdi indsættes giver forskriften en værdi, ganske som for enhver anden funktion.

Skriv et svar til: bestem differentialkvotienten

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.