Matematik

bredde udtrykt ved x

08. marts 2021 af alia90 - Niveau: B-niveau

er der en venlig sjæl derude, som har en metode til at løse følgende opgave, er helt på bar bund. har forsøgt en del men jeg tror simpelthen ikke jeg har noget begreb om hvor man skal starte og min underviser var ikke så samarbejdsvillig.

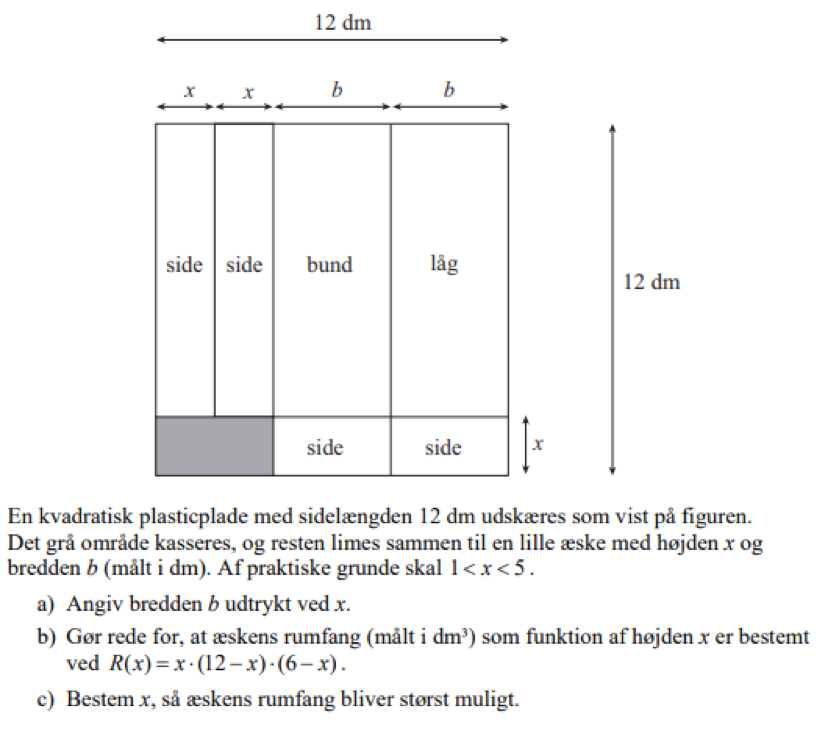
En kvadratisk plasticplade med sidelængden 12 dm udskæres som vist på figuren.
Det grå område kasseres, og resten lmes sammen til en lille æske med højden x og bredden b (målt i dm) - af praktiske grunde skal 1 < x < 5.

a) Angiv bredden b udtrykt ved x.

b) Gør rede for, at æskens rumfang (målt i dm^(3)) som funktion af højden x er bestemt vedR(x)=x*(12-x)*(6-x).

c) Bestem x, så æskens rumfang bliver størst muligt.

Vedhæftet fil: 12 dm mat b.png

Brugbart svar (0)

Svar #1
08. marts 2021 af janhaa

2b + 2x = 12

b + x = 6

b = 6 - x

Brugbart svar (0)

Svar #2
08. marts 2021 af janhaa

R(x) = l*b*h = (12 - x)*(6 - x)*x

R ' (x) = 0

Brugbart svar (0)

Svar #3
08. marts 2021 af janhaa

R ' (x) = 0

dvs:

$x=6-2\sqrt{3}$

Svar #4
08. marts 2021 af alia90

Tusind tak - det ikke for at være til besvær men kan du uddybe det lidt for forstår stadig ikke helt fremgangs måden ?

Brugbart svar (0)

Svar #5
09. marts 2021 af mathon

Brugbart svar (0)

Svar #6
09. marts 2021 af mathon

$\small \small \begin{array}{lllll} \textbf{c)}\\&& R(x)=x\cdot (12-x)\cdot (6-x)=x^3-18x^2+72x\qquad 0<x<6\\\\&& R{\, }'(x)=3x^2-36x+72\\\\& R_{max}\textup{ kr\ae ver bl.a.}\\&& R{\, }'(x)=3x^2-36x+72=0\\\\&& x=\left\{\begin{array}{lll} 6-2\sqrt{3} \approx 2.54\\6+2\sqrt{3} \approx 9.46&\textup{som m\aa \ forkastes} \end{array}\right.\\\\&& R{\, }'(x)=3(x-2.54)(x-9.46)\\\\& \end{array}$

Fortegnsvariation
for $\small R{\, }'(x)$ : + 0 -
x-variation: __________2.54____________6
ekstrema: max
Monotoni
for $\small R(x)$ : voksende aftagende

$\small \begin{array}{llll} \textup{Maksimalt \ae skerumfang}\\ \textup{opn\aa s for }x=6-2\sqrt{3} \end{array}$

Skriv et svar til: bredde udtrykt ved x

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.