Matematik

Linjens parameter fremstilling

31. marts 2021 af Hjælpmigx - Niveau: B-niveau

Hej, jeg har fået denne opgave for, og ved slet ikke, hvordan jeg skal gribe den an.

Nogen der kan hjælpe?

Vedhæftet fil: Linjens parameter fremstilling.docx

Brugbart svar (0)

Svar #1
31. marts 2021 af PeterValberg

Jeg indsætter lige et billede af din opgave, det gør det lidt nemmere at hjælpe
(personligt er jeg ikke så vild med et Word-/pdf-dokument, som jeg skal downloade
for at kunne hjælpe ... jeg foretrækker helt klart vedhæftede, gerne indsatte, billeder)

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #2
31. marts 2021 af PeterValberg

Du skal i første omgang have bestemt mulige koordinater til punktet B
(det kan godt tænkes, at der er mere end ét muligt B).
Opstil en ligning for den cirkel, der har A som centrum og en radius på 10
Bestem nu skæringspunkt(er) mellem denne cirkel og linjen

se video nr. 33 på denne videoliste < LINK >

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #3
31. marts 2021 af mathon

B ligger på kvartcirklen $\small \small x^2+y^2=10^2\quad 0\leq x\leq10\quad 0\leq y\leq10$
i 1. kvadrant, da |AB| = 10
og på
$\small l\textup{:}\quad y=\tfrac{3}{4}x\quad \textup{da }l\textup{ har retningsvektorerne }\bigl(\begin{smallmatrix} 4\\3 \end{smallmatrix}\bigr)\textup{ og }\bigl(\begin{smallmatrix} 1\\\mathbf{{\color{Red} \tfrac{3}{4}}} \end{smallmatrix}\bigr)$

$\small \begin{array}{llllll} \textbf{a)}\\&& \angle A \textup{ er }l\textup{'s retningsvinkel}\\\\&& \angle A =\tan^{-1}\left ( \frac{3}{4} \right )=36.9\degree \end{array}$

Svar #4
31. marts 2021 af Hjælpmigx

Mange tak for svar:))

Brugbart svar (0)

Svar #5
31. marts 2021 af AMelev

Ad #3 For at bestemme vinklen A i ΔABC, skal retningsvinklen for $\overrightarrow{AC}$ trækkes fra retningsvinklen for $l$ .

Alternativ metode

Vinklen A i ΔABC er vinklen mellem $\overrightarrow{AB}$ og $\overrightarrow{AC}$ .
Da både A = O(rigo) og B ligger på $l$ , er vinklen den samme som mellem $\overrightarrow{r_l}=\binom{4}{3}$ og $\overrightarrow{AC}$ .
FS side 11 (50) inkl. figur & (52).
Skitse: Beregn $|\overrightarrow{r_l}|$ og indse, at $\overrightarrow{AB}=2\cdot \overrightarrow{r_l}$
Afsæt A, C og $2\cdot \overrightarrow{r_l}$ ud fra A til B. Forbind A, B og C med rette linjestykker.

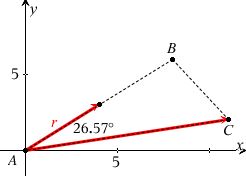
En lidt anden måde at bestemme B på:
$\overrightarrow{AB}=t\cdot \binom{4}{3}$ , t > 0, da B skal ligge i 1. kvadrant, og $\overrightarrow{AB}$ derfor er ensrettet med retningsvektoren for $l$ .
Løs ligningen $|\overrightarrow{AB}|=10$ mht. t.
Indsæt den fundne t-værdi i parameterfremstillingen for $l$ for at bestemme koordinaterne for B.

Vedhæftet fil:Udklip-2.jpg

Brugbart svar (0)

Svar #6
01. april 2021 af mathon

korektion:

$\small \begin{array}{llllll} \textbf{a)}\\&& l\textup{'s retningsvinkel}\\\\&& \angle v =\tan^{-1}\left ( \frac{3}{4} \right )=36.9\degree \end{array}$

Brugbart svar (0)

Svar #7
01. april 2021 af mathon

korrektion:

Brugbart svar (0)

Svar #8
03. april 2021 af mathon

$\small \small \begin{array}{llllll} \textbf{a)}\\&& l\textup{'s retningsvinkel}\\\\&& \angle v =\tan^{-1}\left ( \frac{3}{4} \right )=36.9\degree\\\\&& \angle A=\tan^{-1}\left ( \frac{3}{4} \right )-\tan^{-1}\left ( \frac{2}{11} \right )=26.56\degree \end{array}$

Brugbart svar (0)

Svar #9
03. april 2021 af mathon

eller

$\small \begin{array}{lllll}&& \cos(A)=\frac{\bigl(\begin{smallmatrix} 4\\3 \end{smallmatrix}\bigr)\cdot \bigl(\begin{smallmatrix} 11\\2 \end{smallmatrix}\bigr)}{5\cdot \sqrt{125}}=\frac{50}{5\cdot \sqrt{125}}=\frac{10}{\sqrt{125}}\\\\&& A=\cos^{-1}\left ( \frac{10}{\sqrt{125}} \right )=26.57\degree \end{array}$

Brugbart svar (0)

Svar #10
03. april 2021 af mathon

evt.
$\begin{array}{lllll}& \tan(A )=\frac{\tan(u )-\tan(v )}{1+\tan(u) \cdot \tan(v)}=\frac{\frac{3}{4}-\frac{2}{11}}{1+\frac{3}{4}\cdot\frac{2}{11}}=\frac{\frac{33-8}{44}}{\frac{44+6}{44}}=\frac{25}{50}=\frac{1}{2}&\textup{hvor }u\textup{ og }v\textup{ er retningsvinkler}\\\\& A=\tan^{-1}\left ( \frac{1}{2} \right )=26.57\degree \end{array}$

Skriv et svar til: Linjens parameter fremstilling

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.