Matematik

Dobbelt afledede og den blandede afledede af f

18. maj 2021 af inneedofhomework - Niveau: A-niveau

Hej. Nogen der ved hvordan første opgave a) skal løses?

Tak på forhånd.

Vedhæftet fil: Skærmbillede 2021-05-18 kl. 16.13.36.png

Brugbart svar (0)

Svar #1
18. maj 2021 af mathon

Brugbart svar (0)

Svar #2
18. maj 2021 af AMelev

Se formelsamling side 34 (197)-(200)

a) I TI-Nspire

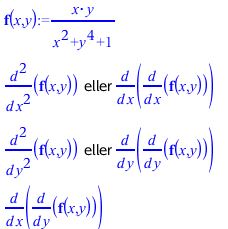
Vedhæftet fil:Udklip-2.jpg

Brugbart svar (0)

Svar #3
18. maj 2021 af mathon

$\begin{array}{lllll} \textbf{a)}\\&& f_x{}'(x,y)=\frac{-y\left (x^2-y^4-1 \right )}{\left ( x^2+y^4+1 \right )^2}\\\\&& f_y{}'(x,y)=\frac{x\cdot \left ( x^2-3y^4+1 \right )}{\left (x^2+y^4+1 \right )^2}\\\\\\&& f_{xy}{}''(x,y)=\frac{-\left(x^4-12x^2\cdot y^4 +\left(y^4+1\right)\cdot \left ( 3y^4-1 \right )\right) }{\left (x^2+y^4+1 \right )^3}\\\\&& f_{xx}{}''(x,y)=\frac{2x\cdot\left ( x^2-3\cdot \left (y^4+1 \right ) \right ) \cdot y}{\left (x^2+y^4+1 \right )^3}\\\\&& f_{yy}{}''(x,y)=\frac{-4x\cdot \left ( 5x^2-3y^4+5 \right )\cdot y^3}{\left ( x^2+y^4+1 \right )^3} \end{array}$

Brugbart svar (0)

Svar #4
18. maj 2021 af mathon

$\small \begin{array}{lllll}&\textup{station\ae re punkter:}\\&& \textup{solve}\left ( \frac{\mathrm{d} }{\mathrm{d} x}(f(x,y))=0\textup{ and } \frac{\mathrm{d} }{\mathrm{d} y}(f(x,y))=0 \right )\\\\&& \left ( -\sqrt{2},-1 \right )\quad \left ( -\sqrt{2},1 \right )\quad \left ( 0,0 \right )\quad \left ( \sqrt{2},1 \right ) \end{array}$

Svar #5
18. maj 2021 af inneedofhomework

Mange tak for hjælpen.

Brugbart svar (0)

Svar #6
19. maj 2021 af mathon

$\small \small \small \small \begin{array}{llllllll} \textbf{c)}\\&& f_{xx}{}''(x,y)=\frac{2x\cdot\left ( x^2-3\cdot \left (y^4+1 \right ) \right ) \cdot y}{\left (x^2+y^4+1 \right )^3}&=&r(x,y)\\\\&& f_{xy}{}''(x,y)=\frac{-\left(x^4-12x^2\cdot y^4 +\left(y^4+1\right)\cdot \left ( 3y^4-1 \right )\right) }{\left (x^2+y^4+1 \right )^3}&=&s(x,y)\\\\&& f_{yy}{}''(x,y)=\frac{-4x\cdot \left ( 5x^2-3y^4+5 \right )\cdot y^3}{\left ( x^2+y^4+1 \right )^3}&=&t(x,y) \\\\& \textbf{art:}\\&& r(-\sqrt{2},-1)\cdot t(-\sqrt{2},-1)-s(-\sqrt{2},-1)^2>0&&\textup{og }r(-\sqrt{2},-1)<0\Rightarrow &\textup{ lokalt maksimum}\\\\&& r(-\sqrt{2},1)\cdot t(-\sqrt{2},1)-s(-\sqrt{2},1)^2>0&&\textup{og }r(-\sqrt{2},1)>0\Rightarrow &\textup{ lokalt minimum}\\\\&& r(0,0)\cdot t(0,0)-s(0,0)^2<0&&\qquad\qquad\qquad\qquad\! \! \Rightarrow &\, \, \textup{saddelpunkt}\\\\&& r(\sqrt{2},1)\cdot t(\sqrt{2},1)-s(\sqrt{2},1)^2>0&&\textup{og }r(\sqrt{2},1)<0\Rightarrow & \textup{ lokalt maksimum}\\\\&& \end{array}$

Skriv et svar til: Dobbelt afledede og den blandede afledede af f

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.