Matematik
Nogle der kan hjælpe. Forstår ikke helt hvorfor toppunktsformlen er anvendelig. Derudover forstår jeg ikke 0≤x≤2500.
•Forklar hvorledes toppunktsformlen er anvendelig i en besvarelse af nedenstående problemstilling:
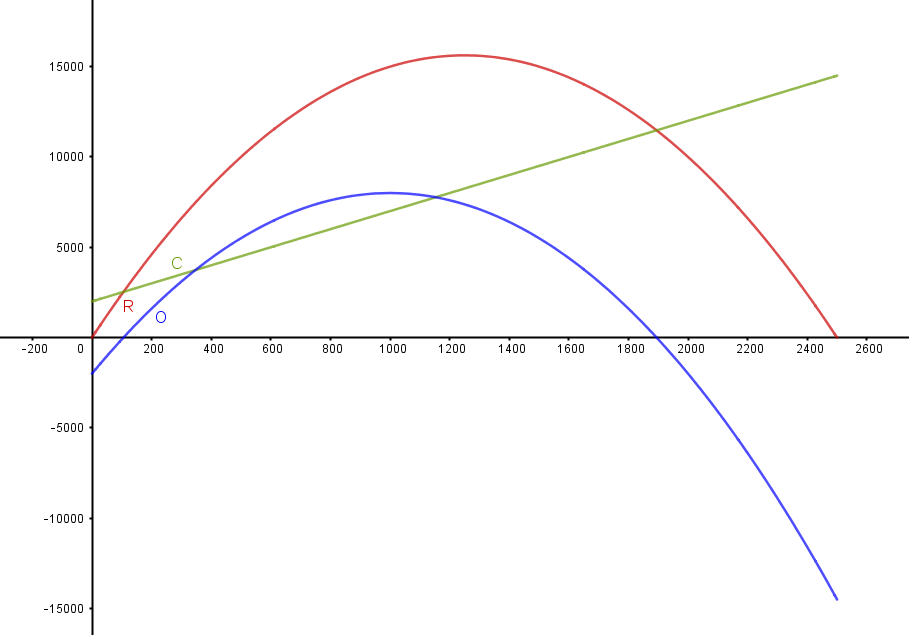
Et firma har konstateret, at omsætningen R(x) for en bestemt vare er en funktion af afsætningen x, nemlig R(x) = -0.01x^2 + 25x, hvor 0≤x≤2500.
•De samlede omkostninger C(x) for den samme vare er en funktion af afsætningen med forskriften
• C(x) = 5x + 2000, hvor 0≤x≤2500.
•Bestem overskudsfunktionen
•Bestem den afsætning der giver det størst mulige overskud
•Bestem det størst mulige overskud
Svar #1
21. juni 2021 af PeterValberg
Intervallet, du ikke forstår, er definitionsmængden for R
Du kan bruge toppunktsformlen, fordi grafen for R
vil være en parabel, der vender parabelgrenene nedad,
dermed bliver toppunktet, det sted, hvor funktionsværdien
vil være størst, - hvilket du med garanti skal benytte i de andre spørgsmål
Svar #2
21. juni 2021 af PeterValberg
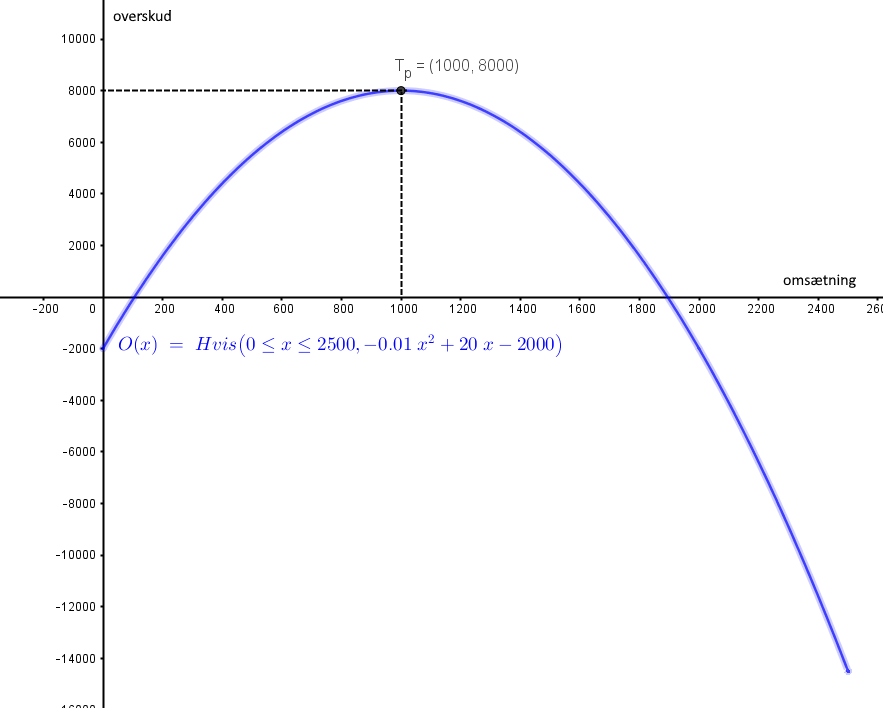
Jeg tænker, at overskudsfunktionen O er differensen
på omsætningsfunktionen R og omkostningsfunktionen C
defineret i intervallet 0 ≤ x ≤ 2500
Grafen for overskudsfunktionen O er en parabel, hvor parabelgrenene vender nedad
den afsætning xT, der giver det største overskud, og selve overskuddet O(xT) kan
dermed bestemmes vha. toppunktformlen
Svar #4
21. juni 2021 af nielsensend212 (Slettet)
Hej tak for hjælpen, det giver mening det du skriver, men forstår stadig ikke hvordan man bestemer den afsætning der giver det størst mulige overskud?
Svar #5
21. juni 2021 af PeterValberg
Du skal slet og ret bestemme toppunktet for overskudsfunktionen
x-koordinaten er den omsætning, der giver det største overskud
y-koordinaten er det største overskud, der kan opnås
Sådan bestemmer du toppunktet for en parabel < LINK >
Skriv et svar til: Nogle der kan hjælpe. Forstår ikke helt hvorfor toppunktsformlen er anvendelig. Derudover forstår jeg ikke 0≤x≤2500.
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.