Matematik

Fuldstændige/partikuler løsning til differentialligningen, og hvor hældtallet er størst.

17. november 2021 af Annapetra - Niveau: A-niveau

Bestem den fuldstændige løsning til denne diffirentialligning y'=-4x^3 y + 8x^3.

Og find den partikulere løsning hvor y(1)=3.

Find det punkt på løsningen hvor hældningskoefficienten er størst.

Svar #1
17. november 2021 af Annapetra

Efter vi finder den partikuler løsning, har jeg brug for at finde hældningskoefficienten før vi finder hvor den er størt.

Brugbart svar (0)

Svar #2
17. november 2021 af janhaa

$\int \frac{dy}{2-y}= \int 4x^3 dx\\ \\-\ln(2-y)= x^4+c\\ Etc$

Svar #3
17. november 2021 af Annapetra

jeg forstår ikke helt janhaa

Brugbart svar (0)

Svar #4
17. november 2021 af janhaa

$2-y=c*e^{-4x^3}\\ \\ y=2+c*e^{-4x^3}$

y(1)=3

c = e⁴

Thus;

$2-y=c*e^{-4x^3}\\ \\ y=2+c*e^{-4x^3}\\ \\ y=2+e^{4-4x^3}$

Brugbart svar (0)

Svar #5
17. november 2021 af Soeffi

#0. Hvilke hjælpemidler har du?

Brugbart svar (0)

Svar #6
17. november 2021 af janhaa

#3
jeg forstår ikke helt janhaa

y' = 4x³(2-y)

$\int \frac{dy}{2-y}=\int 4x^3 dx$

Brugbart svar (0)

Svar #7
17. november 2021 af janhaa

y ' = -4

Svar #8
17. november 2021 af Annapetra

hvordan finder man så den partikukær løsning, hældningskoffficienten og hvor den er størst?

Brugbart svar (1)

Svar #9
17. november 2021 af Soeffi

#0. Fuldstændig løsning:

$\frac{dy}{dx}=-4x^3 y + 8x^3\Leftrightarrow \frac{dy}{dx}=4x^3 \cdot (-y + 2)\Leftrightarrow$

$\left ( y\neq 2 \wedge \frac{1}{2-y}\cdot \frac{dy}{dx}=4x^3 \right ) \vee \left ( y=2 \wedge \frac{dy}{dx}=0 \right ) \Leftrightarrow$

$\left ( y\neq 2 \wedge \int \frac{1}{2-y}\cdot dy=\int4x^3\cdot dx \right ) \vee \left ( y=2 \right ) \Leftrightarrow$

$\left ( y\neq 2 \wedge -ln(|2-y|) =x^4+c \right ) \vee \left ( y=2 \right ) \Leftrightarrow$

$\left ( y\neq 2 \wedge |2-y| =exp(-x^4+c) \right ) \vee \left ( y=2 \right ) \Leftrightarrow$

$\left (y < 2 \wedge 2-y =e^{-x^4+c} \right ) \vee \left (y > 2 \wedge -2+y =e^{-x^4+c} \right ) \vee \left ( y=2 \right ) \Leftrightarrow$

$\left (y < 2 \wedge y =2-Ce^{-x^4} \right ) \vee \left (y > 2 \wedge y =Ce^{-x^4}+2 \right ) \vee \left ( y=2 \right ) ,C>0\Leftrightarrow$

$y=\begin{Bmatrix} 2+Ce^{-x^4},y<2,C<0 \\ 2+Ce^{-x^4},y=2,C=0 \\ 2+Ce^{-x^4},y>2,C>0 \end{Bmatrix} \Leftrightarrow y= 2+Ce^{-x^4},C\in \mathbb{R}$

Particulær løsning:

$y_1(1)=3 \Rightarrow 2+Ce^{-1}=3 \Leftrightarrow Ce^{-1}=1\Leftrightarrow C=e$

$y_1(x)= 2+e^{1-x^4}$

Graf i Maple:

Vedhæftet fil:Skærmbillede 2021-11-17 kl. 20.51.41.png

Brugbart svar (0)

Svar #10
18. november 2021 af Soeffi

#9. Rettelse:...
$\\ \left (y < 2 \wedge y =2-ke^{-x^4} \right ) \vee \left (y > 2 \wedge y =ke^{-x^4}+2 \right ) \vee \left ( y=2 \right ) ,\\\\hvor\;k=e^c>0\Leftrightarrow$

$y=\begin{Bmatrix} 2+Ce^{-x^4},y<2,C<0 \\ 2+Ce^{-x^4},y=2,C=0 \\ 2+Ce^{-x^4},y>2,C>0 \end{Bmatrix} \Leftrightarrow y= 2+Ce^{-x^4},\;hvor\;C\in \mathbb{R}$

...

Brugbart svar (0)

Svar #11
20. november 2021 af Soeffi

#0. Største hældningskoefficient for y₁(x):

$y'(x)=-4x^3e^{1-x^4}$

$y_1''(x)=(-3 +4 x^4) \cdot 4x^2 \cdot e^{1-x^4}=0\Leftrightarrow (-3 +4 x^4) \cdot 4x^2 =0\Leftrightarrow$

$-3 +4 x^4=0 \vee 4x^2 =0\Leftrightarrow x= \pm \sqrt[4]{3/4} \vee x=0$

$y'(0)=0$

$\\y'(-\sqrt[4]{3/4})\approx y'(-0,9306) \approx 3^{3/4}4^{1/4}e^{1/4}=4,1392$

$y'(\sqrt[4]{3/4})=-4,1392$

Punkt med størst hældning:

$(x,y)=(-0,9306;4,1392)$

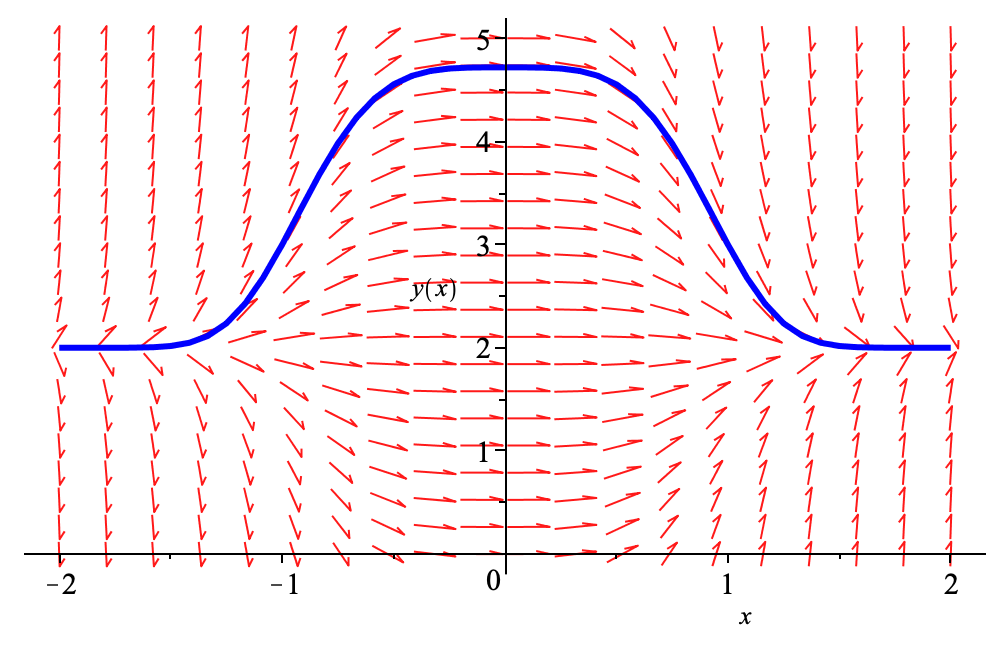
Skriv et svar til: Fuldstændige/partikuler løsning til differentialligningen, og hvor hældtallet er størst.

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.