Matematik

parabler og 2. gradspolynomier

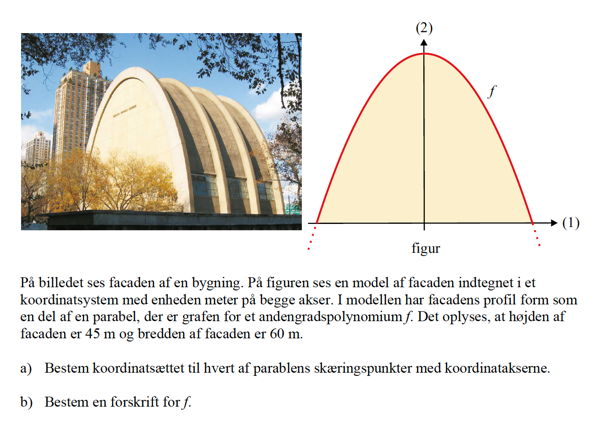
10. januar 2022 af maddie123 - Niveau: C-niveau

på billedet ses facaden af en bygning. på figuren ses en model ses en model af facaden indtegnet i et kordinatsystem med enheden meter på begge akser. i modellen har facadens profil form som en del af en parabel der er grafen for et 2. gradspolonymie F. Det oplyses at, højden af facaden er 45 meter og breden af facaden er 60 meter.

a) bestem kordinatsættet til hvert af parablens skæringspunkter med kordinat akserne

b) bestem en forskrift for F

Brugbart svar (0)

Svar #1
10. januar 2022 af peter lind

Vedlæg hele opgaven som en fil i billedfil eller pdf fil

Svar #2
10. januar 2022 af maddie123

her

Vedhæftet fil:2.gradspolynomier.docx

Brugbart svar (0)

Svar #3
11. januar 2022 af PeterValberg

Jeg indsætter lige et screendump af opgaveteksten,
det er lidt nemmere ... bemærk, at det ikke er alle herinde,
der kan åbne *.docx dokumenter ... et screendump havde været bedre

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #4
11. januar 2022 af ringstedLC

$\begin{align*} F(x) &= a\cdot x^2+c \\ F(0)=45 &= a\cdot 0^2+c\Rightarrow c=\;? \\ F\left ( \tfrac{60}{2} \right )=0 &= a\cdot \left ( \tfrac{60}{2} \right )^2+c\Rightarrow a=\;? \end{align*}$

Brugbart svar (0)

Svar #5
11. januar 2022 af PeterValberg

a) Bredden er 60 m og parablen er symmetrisk omkring y-aksen
Koordinatsættene til skæringspunkterne med x-aksen må derfor være
(30, 0) og (-30, 0)

Højden er opgivet til 45 m, skæringspunktet med y-aksen må derfor være (0, 45)

b) parablen følger modellen f(x) = ax² + bx + c og du kender allerede c = 45
Indsæt værdien for c samt de to kendte skæringspunkter med x-aksen i modellen
og bestem værdierne for hhv. a og b som to ligninger med to ubekendte

Eller gør som angivet i #4 (det er noget nemmerre)

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #6
22. september 2022 af nikita0876

hvordan vil i sætte denne andengradsligning op? og vil gerne regne den som to ligninger med to ubekendte

Brugbart svar (0)

Svar #7
23. september 2022 af ringstedLC

$\begin{align*} 0 &= a\cdot (-30)^2+b\cdot (-30)+45 \\ 0 &= a\cdot 30^2+b\cdot 30+45\end{align*}$

Fx med substitution:

$\begin{align*} 0 &= a\cdot (-30)^2+b\cdot (-30)+45 \\ b &=\frac{-900a-45}{-30}=\frac{300a+15}{10} \\ 0 &= a\cdot 30^2+\frac{300a+15}{10}\cdot 30+45 \Rightarrow a=-...\\ b &= \frac{300\cdot a+15}{10}\Rightarrow b=... \end{align*}$

Men det ville være tidsspilde:

$\begin{align*} \textup{Toppunkt}:(0,45)\Rightarrow x_T=0 &= \frac{-b}{2a} \\ 0 &= \frac{b}{2a}\\0 &= b \\ \Rightarrow f(30)=f(-30)=0 &= a\cdot 30^2+45\Rightarrow a=...\end{align*}$

Skriv et svar til: parabler og 2. gradspolynomier

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.