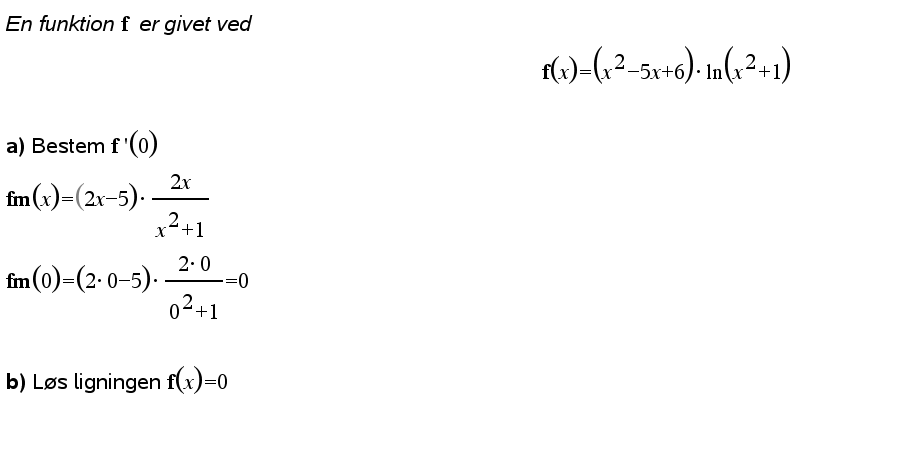Matematik

Løs ligningen f(x)=0

30. marts 2022 af MCS1 - Niveau: A-niveau

Hjælp til b

Vedhæftet fil: Screenshot 2022-03-30 013048.png

Svar #1
30. marts 2022 af MCS1

Brugbart svar (0)

Svar #2
30. marts 2022 af SuneChr

Der er to faktorer, som vi, hver for sig, finder 0-punkter for.
Find dem for andengradspolynomiet og for logaritmefunktionen.
Det samlede antal er funktionens 0-punkter.
Vi har benyttet 0-reglen, som er vigtig at kunne.

Brugbart svar (0)

Svar #3
30. marts 2022 af SuneChr

a) Et produkt (gh) differentieres:
(gh)' = gh' + g'h
Kig på produktet igen.

Brugbart svar (0)

Svar #4
30. marts 2022 af mathon

$\small \begin{array}{lllllll} f{\, }'(x)=\left ( 2x-5 \right )\cdot \left ( \ln(x^2+1) \right )+\left ( x^2-5x+6 \right )\cdot \frac{2x}{x^2+1}\\\\ f{\, }'(0)=\left ( 2\cdot 0-5 \right )\cdot \left ( \ln(0^2+1) \right )+\left ( 0^2-5\cdot 0+6 \right )\cdot \frac{2\cdot 0}{0^2+1}=-5\cdot 0+6\cdot \frac{0}{1}=0 \end{array}$

Brugbart svar (0)

Svar #5
30. marts 2022 af mathon

$\small \small \small \begin{array}{lllllll} \small &&f(x)=(x-3)(x-2)\cdot \ln(x^2+1)\\\\&& f(x)=0\\\\ \textup{kr\ae ver}\\& f(x)=0&\Leftrightarrow x=\left\{\begin{matrix} 0\\2 \\ 3 \end{matrix}\right. \end{array}$

Skriv et svar til: Løs ligningen f(x)=0

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.