Matematik
Cirklens hastighedsvektor
Hej. Jeg ville lige høre, om der var nogle der evt. kunne forklare/bevise, hvorfor længden af hastighedsvektoren for en cirkel er uafhængig af parameteren t?
Svar #2
16. maj 2022 af SuneChr
For en cirkel med parameterfremstillingen
x = rcos t
y = rsin t
er hastigheden tværvektoren af den til ethvert punkt på cirkelperiferien svarende radiusvektor.
Længden af hastighedsvektoren er den samme som længden af radiusvektoren for cirkelfremstillingen,
|r| = |r'|
Vi har jo idiotformlen: cos2 t + sin2 t = 1 for 0 ≤ t < 2π
Svar #3
16. maj 2022 af ringstedLC
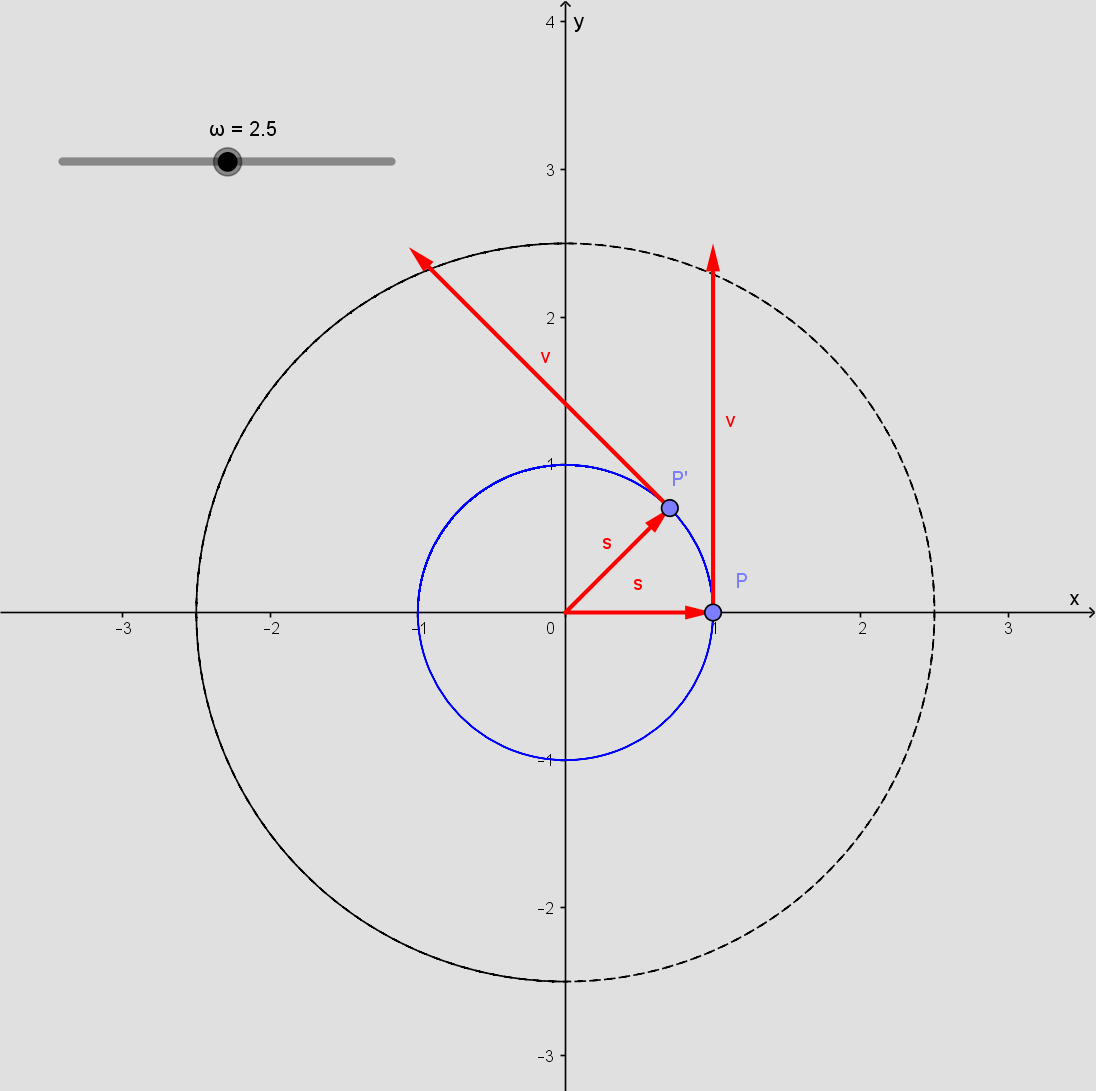
t er kun medbestemmende for hvor på cirklen P ligger.
ω og r bestemmer hvor lang hastighedsvektoren v er.
Svar #4
16. maj 2022 af peter lind
Du mener nok en jævn cirkelbevægelse. Det ligger nemlig i ordet jævn altså er med konstant fart.
Hvis du har en kugle, der kan bevæge sig på en rille skåret ud i et crkelformet spor og du bevæger den med fingeren er den jo alt andet end jævn
Skriv et svar til: Cirklens hastighedsvektor
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.





