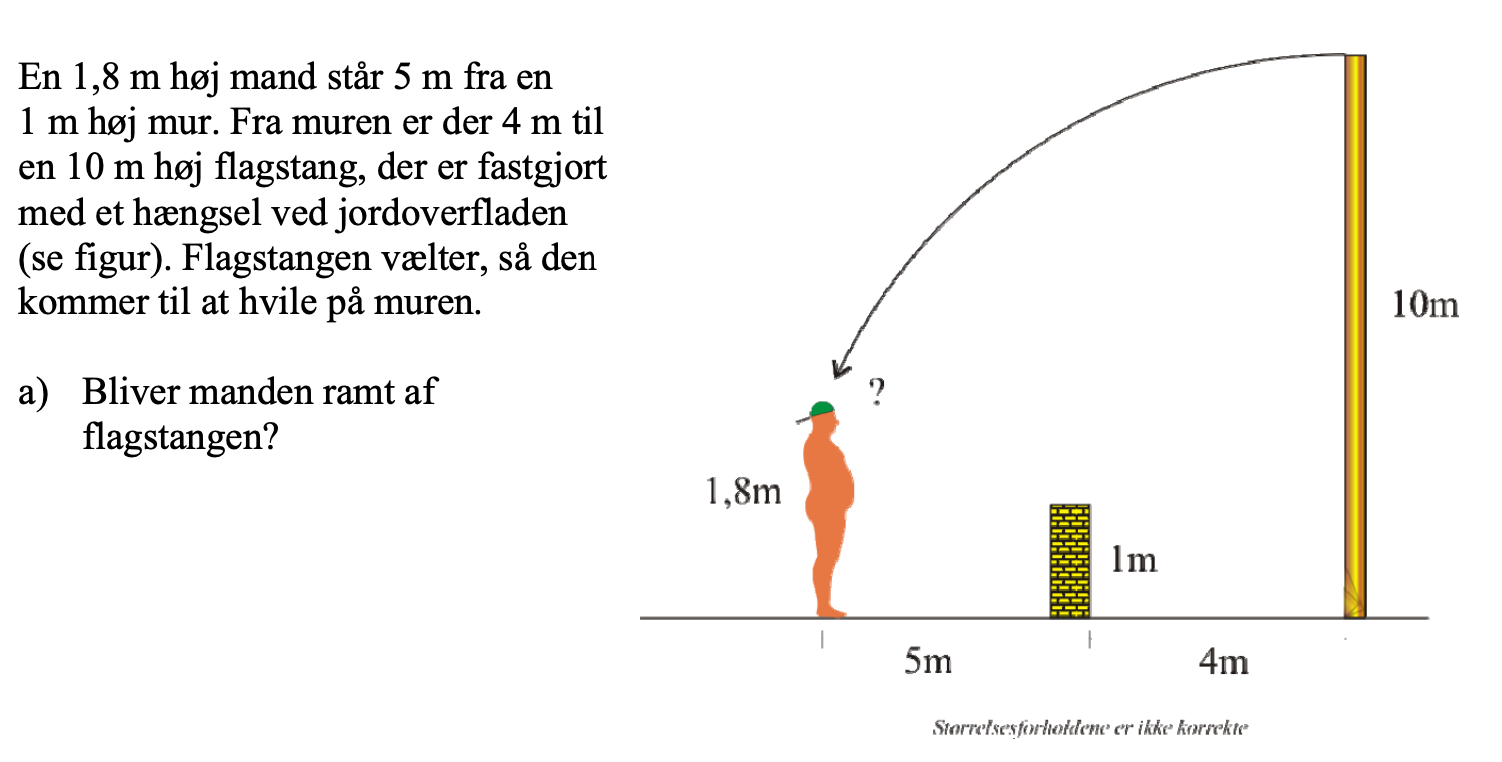
Rammer flagstangen manden

Hey Sara. Jeg ville nok bruge Pythagoras' sætning:

c^2 = a^2 + b^2

c^2 = 10^2 + 5^2 c^2 = 100 + 25 c^2 = 125 c = √125 c ≈ 11,18 meter. Den rammer altså ikke manden, hvis man bruger Pythagoras.

hypotenusen:

hypotenusen^2 = katet^2 + katet^2 hypotenusen^2 = 5^2 + 9^2 hypotenusen^2 = 25 + 81 hypotenusen^2 = 106 hypotenusen = √106 ≈ 10,30 meter

Brug ensvinklede trekanter til at finde ud af, hvor højt oppe flagstangen er dér, hvor manden står.

#1 Du skriver ikke, hvilke trekanter, du regner på. Det ser ud  som om du bare tager to af tallene, kvadrerer dem, lægger dem sammen og uddrager kvadratroden uden at gøre rede for, at det er relevant at bruge netop de to tal.

a) Da størrelsesforholdene ikke er korrekte, ville jeg starte med at undersøge om flagstangen i det hele taget kan nå manden ved at beregne hypotenusen i den trekant, hvor manden og hans afstand til hængslet er kateter.

Det er hurtigere at undersøge, om stangen kan komme langt nok ned, hvis den er lang nok. Det kræver kun en multiplikation og en division. Man kan endog simplificere det lidt ved at se, om manden ville blive ramt, hvis han stod en meter længere fremme.

Den mindste trekant består af det første stykke på jorden, muren og flagstangen, der hviler på muren. Den anden består af hele stykket på jorden, lodret op til flagstangen og flagstangen.

Denne metode giver resultatet ved simpel hovedregning.

Jeg regner med, at flagstangen er så stiv, at vi kan se bort fra deformation af stangen.

Hvis manden vil beholde kasketten på og i øvrigt undgå hjernerystelse,
må han ikke komme nærmere muren^* end 3,2 m.
____________
_{*   (Muren antages ingen udstrækning at have, undtagen i højden).}

#0. Se også https://www.studieportalen.dk/forums/thread.aspx?id=1916146.

Hvis muren ikke var der, ville flagstangen ramme manden. 1. katete: de 9 m fra flagstangen, 2. katete: mandens højde. Hypotenusen er kortere end flagstangen.

Hvis flagstangen var 9,1m og der ikke var nogen mur, ville flagstangen stadig ramme manden, men ikke i hovedet