Matematik

Vurdering af fejlen ved Taylors formel

04. marts 2017 af Rossa - Niveau: Universitet/Videregående

Hej derude. Jeg har en opgave, hvor jeg ikke kan finde en løsning til det.
Det kan være, at opgaven ikke forstået rigtigt, men her kan man se, hvad jeg gør forkert, eller det jeg misforstå.
Opgaven lyder:

Opstil Taylorpolynomiet P₃ af tredje grad for Artanh(y) med udviklingspunktet y = 0.

Vis at |Artanh(y) − P₃(y)| < 1/8 for alle y ∈ [−1/2, 1/2].

Jeg forsøger, at opstille en ligning, som Artanh(y) − P₃(y)| -1/8 =0, men ligning har ikke reelle rødder.
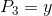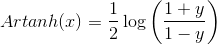
Altså har vi P_3 =y og $A rtanh(x) = \frac{1}{2} \log\left(\frac{1+y}{1-y} \right)$

Brugbart svar (0)

Svar #1
04. marts 2017 af Stats

- - -

Mvh Dennis Svensson

Brugbart svar (0)

Svar #2
04. marts 2017 af Stats

Man skal anvende Taylor med restled (Lagrange restled)

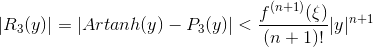
$|R_3(y)|=|Artanh(y)-P_3(y)|< \frac{f^{(n+1)}(\xi )}{(n+1)!}|y|^{n+1}$

Du har n = 3, og skal derfor udregne Artanh⁽³⁺¹⁾(ξ) = (24y+24y³)/(1-y²)⁴

Den største værdi findes i endepunkterne og du får Artanh⁽⁴⁾(1/2) = 1280/27.

Dermed er formlen:

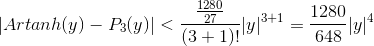
$|Artanh(y)-P_3(y)|< \frac{\frac{1280}{27}}{(3+1)!}|y|^{3+1}=\frac{1280}{648}|y|^4$

Ok.. Nu er det simpelt at finde ud af, om |Artanh(y) - P₃(y)| < 1/8

Vi skal egentlig bare konkludere at

$\frac{1280}{648}|y|^4< \frac{1}{8} \text{ for }y\in[-1/2,1/2]$

Vi opdager, at den maksimale fejl må være i yderpunkterne (når y vokser, så vokser fejlen.)

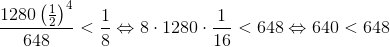
$\frac{1280\left(\frac{1}{2}\right)^4}{648}<\frac{1}{8}\Leftrightarrow 8\cdot1280\cdot\frac{1}{16}<648\Leftrightarrow 640<648$

Som er korrekt...

- - -

Mvh Dennis Svensson

Brugbart svar (0)

Svar #3
04. marts 2017 af LeonhardEuler

#2: Der skal argumentere for at den største numeriske værdi antages i endepunkterne.

Brugbart svar (0)

Svar #4
04. marts 2017 af AskTheAfghan

Hvis f opfylder særlige kriterier, har du nok lært, at f(x) = P_n,a(x) + R_n(x) omkring x = a, hvor R_n er et restled. Restleddet kan være R_n(x) = (f⁽ⁿ⁺¹⁾(q)/(n+1)!)(x - a)ⁿ⁺¹ for et q i (a, x), bedre kendt som Lagranges restled.

Sættes f(y) = artanh(y), har du |f(y) - P_3,0(y)| = |R₃(y)| = |(q³ + q)/(1 - q²)⁴||y|⁴ for et q ∈ (0, y). Nu skal du begynde med at undersøge noget på højresiden ved at lade y være givet med |y| ≤ 1/2.

For eksempel, du har |y|⁴ ≤ 1/16, og tælleren giver 0 < q³ + q < y³ + y ≤ 5/8 (hvorfor?). Undersøg selv med nævneren. Hvis du har undersøgt det, vil du indse, at brøken er positiv. For at gøre det lettere for dig, må du komme frem til at vise, at |(q³ + q)/(1 - q²)⁴||y|⁴ < 10/81. Dette er klart mindre end 10/80 = 1/8.

Brugbart svar (0)

Svar #5
05. marts 2017 af AskTheAfghan

Fortsættelse af #4. Bevis selv at 3/4 ≤ 1 - y² < 1 når |y| ≤ 1/2. Idet 0 < q < y, må 0 < q² < y², og dermed er 1 - y² < 1 - q² < 1 for alle y. Specielt er 3/4 ≤ 1 - y² < 1 - q² < 1 for alle |y| ≤ 1/2.

Du har da fået en række vurderinger til nævneren, nemlig 1 < 1/(1 - q²)⁴ < 1/(1 - y²)⁴ < 1/(3/4)⁴ for alle |y| ≤ 1/2. Vis så at |f(y) - P_3,0(y)| < 10/81 for alle |y| ≤ 1/2.

Skriv et svar til: Vurdering af fejlen ved Taylors formel

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.