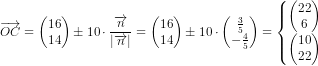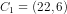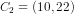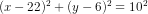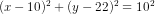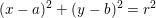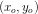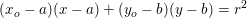Matematik
Bestemmelse af ligning for cirkel
Hej
Har nu siddet med denne opgave i et stykke tid, men kan ikke helt fatte hvordan det skal løses. Opgaven er 3-delt, og jeg har problemer med den sidste del.
Først del: En cirkel har ligningen 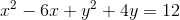 . Bestem centrum og radius for cirklen, og tegn cirklen.
. Bestem centrum og radius for cirklen, og tegn cirklen.
Denne del har jeg gjort, og jeg fik cirklens centrum til at være 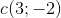 og
og 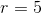
Anden del: Punktet 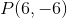 ligger på cirklen. Bestem en ligning for tangenten
ligger på cirklen. Bestem en ligning for tangenten 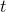 til cirklen i punktet
til cirklen i punktet 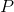 .
.
Dette har jeg løst, og jeg fik ligningen for tangenten 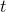 til at være
til at være 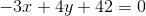
Tredje del: Linjen 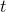 er også tangent til en anden cirkel, der har centrum i punktet
er også tangent til en anden cirkel, der har centrum i punktet 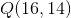 . Bestem en ligning for denne cirkel.
. Bestem en ligning for denne cirkel.
Som sagt er det tredje spørgsmål som jeg ikke helt forstår, og ville blive meget glad hvis en venlig person gad at hjælpe mig.
Svar #1
21. august 2017 af SuneChr
Bring t på normalform og indsæt deri Q. Afstanden er da lig med radius i cirklen med centrum i Q.
Svar #2
21. august 2017 af PresidentDungeon
Jeg kan nogenlunde forstå hvad du mener, men jeg må ærligt indrømme, at jeg følger mig lidt tabt...
Svar #4
21. august 2017 af PresidentDungeon
Jeg kan godt se, at hvis man udregner dette får man en radius på 10, men jeg forstår ikke helt hvordan det hænger sammen?
Ellers tak for hjælpen indtil videre.
Skriv et svar til: Bestemmelse af ligning for cirkel
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.



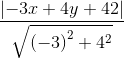
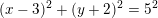 har i punktet
har i punktet 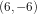
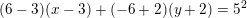
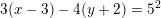
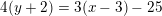
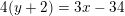
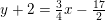
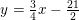
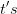 positive og negative halvplan, som
positive og negative halvplan, som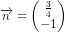
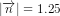
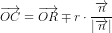 hvor
hvor 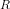 er røringspunktet (16,14)
er røringspunktet (16,14)