Matematik
Monotoniforhold: Anvendelse..
Hej :-)
Der er dette eksempel i min bog:
Eks) Optimeringsopgave
Blikplade 40 cm x 50 cm
skal man fremstille en æske uden låg ved at skære kvadratiske hjørnestykker bort og dernæst folde siderne op. Ønsket er at fremstille en æske med så stort rumfang som muligt.
Vi bortskærer kvadrater med sidelængde x cm. Den æske der opstår ved at bukke siderne op får længden 40 - 2x cm og bredden 50 - 2x cm. Æskens rumfang V bliver derfor
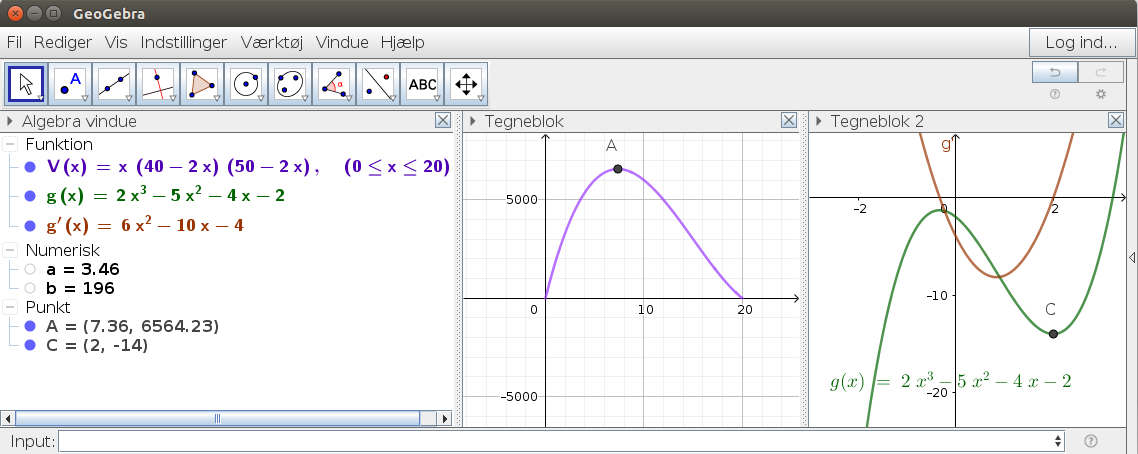
V(x)=x(40-2x)(50-2x)
Vi skal bestemme maksimumsværdien for V(x) i intervallet [0;20]. Da blikpladens korte side er 40 cm. lang kan x ikke overstige 20 cm.
På cas tegnes grafen for funktionen og maksimumsstedet og maksimumsværdien aflæses til henholdvis x=7,362 og V(7,362)=6564,23
Æskens højde, bredde og længde bliver henholdvis
x=7,362 cm, 40-2x=25,276 cm og 50-2x=35,276 cm
Dens rumfang er 6564cm^3 =6,564 liter.
Mit spørgsmål lyder på hvad funktionen er? altså den de tegner grafen og aflæser udfra.
Andet spørgsmål lyder på hvad intervallet har at sige? hvor skal de 20cm bruges?
Udover dette er der en opgave jeg skal løse som lyder..
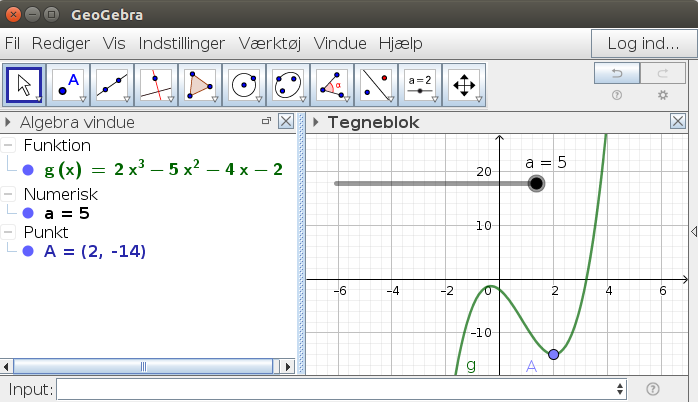
1) Om funktionen g(x) = 2x^3 + ax^2−4x−2, hvor a er en konstant, er det givet, at den har lokalt minimum for x = 2.
Bestem a.
//Jeg har en ide om at jeg ska indsætte 2 på x's plads, og isolere a, er det korrekt? i så fald, er der mon en der kan vise mig hvordan udregningen ser ud?
Tak på forhånd. :-))
Svar #1
22. oktober 2017 af peter lind
i V(x) skal du også undersøge om V(20) er et maksimum
Find g'(x) og løs ligningen g'(2)=0
Svar #2
22. oktober 2017 af StoreNord
#0 Funktionen, grafen tegnes udfra er: V(x)=x(40-2x)(50-2x)
her kan man aflæse, at V(7,362)=6564,23
Hvis op-bukket er er ≥ 20, blir der ikke noget rumfang.
Opgave 1:
Svar #5
29. oktober 2017 af aliciaemilien
Ja, eller ikke for meget nødvendigvis, jeg ved bare ikke hvor du har det fra..
Du har skrevet: g(x)=2x^3-5x^2-4x-2
Men i opgaven lyder den g(x) = 2x^3 + ax^2−4x−2
Svar #9
29. oktober 2017 af StoreNord
Prøv at differentiere f(x) for at finde dens lokale minimum. Du får en 2. gradsligning med et a. Løs denne med hensyn til x. Du får et udtryk med et a. Værdien af dette udtryk er 2. Opstil denne ligning (med et a).
Løs så ligningen ved at kvadrere begge sider.
Svar #10
29. oktober 2017 af aliciaemilien
Det vil jeg lige prøve. Tak :)!
Jeg kan fornemme du er ret god til Geogebra.. jeg sidder lige nu med en opgave hvor jeg skal bruge noget der hedder minimumsfaciliteten i CAS, men jeg kan ikke finde den.
I CAS skal jeg tegne grafen for f(x)=2πx^2+800/x
"Ved hjælp af minimums faciliteten finder du ud af at minimum for x=... dette er den radius man bør vælge på dåsen."
Er det noget du kan hjælpe med? ^^'
Svar #11
29. oktober 2017 af StoreNord
Rettelse til #9
Prøv at differentiere f(x) for at finde dens lokale minimum. Du får en 2. gradsligning med et a. Løs denne med hensyn til x. Du får et udtryk med et a. Værdien af dette udtryk er 2. Opstil denne ligning (med et a).
Løs så ligningen ved at kvadrere begge sider.
Løs så ligningen ved at gange begge sider med 12
isolere kvadratroden
kvadrere begge sider og
løse endnu en 2. gradsligning. :)
Geogebra er meget nemmere!
Svar #12
29. oktober 2017 af aliciaemilien
Modtaget :-)
Jeg synes ikke noget af det her er nemt D:
Jeg troede faktisk, at det var CAS i geogebra jeg skulle bruge?
Svar #14
29. oktober 2017 af StoreNord
Nej, du behøver ikke at bruge CAS.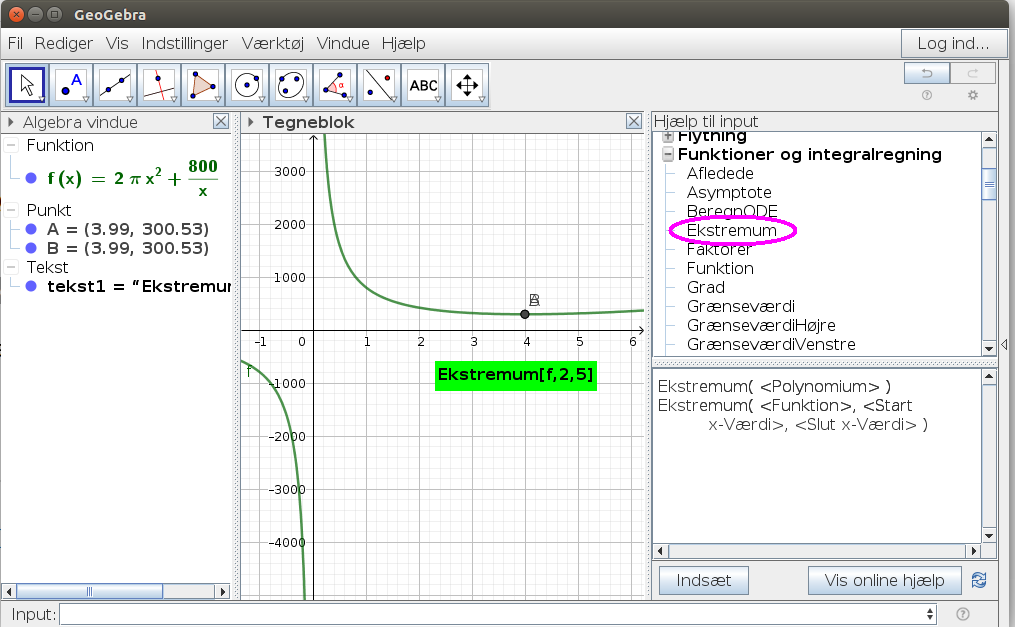
Svar #15
29. oktober 2017 af aliciaemilien
Men det giver mig jo 2 punkter, efter hvad jeg ved skal jeg bruge et tal? :)
Jeg har brugt eksemplet på billedet, at gå ud fra. Opgaven jeg skal løse lyder
"Hvilken højde og hvilken radius (2 dec.), skal en cylinderformet blikdåse have, når den skal indeholde 400 ml og have mindst mulig overflade? Dåsen skal have både bund og låg."
Jeg er kommet frem til følgende
Bunden og låget har hvert et areal πr^2
Dåsens omkreds er 2πr
Dens krumme overflade 2πrh
Det samlede overfladeareal er derfor a = 2πr^2+2πrh
Forudsætningen er, at rumfanget er 400 cm^3
Derfor gælder det, at πr^2h=400
Jeg isolere nu h h=400/πr^2
og indsætter dette i formlen for A, dette bliver nu en funktion af r
A(r)=2πr^2+2πr*400/πr^2=2πr^2+800/r
Ser jeg på eksemplet skal jeg nu tegne grafen i cas, bruge minimumsfaciliteten og komme frem til et tal, som så er den radius jeg bør bruge.
Er jeg helt gal på den?
Svar #16
29. oktober 2017 af StoreNord
At jeg fik både punkt A og punkt B, skyldes at jeg rystede på hånden. Du skal bare skrive:
Ekstremum[f,0,10] eller her blot Ekstremum[f]
Ofte er der flere ekstremer, men ikke her.
I Geogebra er CAS en anden tilstand, som du kan komme i ved at klikke på vis og vælge CAS.
Prøv også Vis->3D grafik.
Svar #17
29. oktober 2017 af aliciaemilien
#11Rettelse til #9
Prøv at differentiere f(x) for at finde dens lokale minimum. Du får en 2. gradsligning med et a. Løs denne med hensyn til x. Du får et udtryk med et a. Værdien af dette udtryk er 2. Opstil denne ligning (med et a).
Løs så ligningenved at kvadrere begge sider.
Løs så ligningen ved at gange begge sider med 12
isolere kvadratroden
kvadrere begge sider og
løse endnu en 2. gradsligning. :)Geogebra er meget nemmere!
g(x) = 2x3 + ax2−4x−2
n*x^n-1
3*2x^3-1
6x^3-1
6x^2
n*x^n-1
2*ax^2-1
2ax
-4
-2 = en konstant = 0
g’(x)=6x^2 +2ax-4
g’(2)=6*2^2 +2a*2-4 = 12^2 +4a-4
Er dette korrekt? jeg er lidt i tvivl om hvordan jeg kommer videre herfra. :d
Svar #18
29. oktober 2017 af aliciaemilien
#16Når jeg skriver ekstremum[f] i input får jeg det her
Svar #19
29. oktober 2017 af aliciaemilien
Måske fordi at jeg skulle tage at skrive ekstremum[a] i stedet.. nevermind :-D
Men det ændre jo ikke på, at der stadig er to tal (3.99,300.53), og jeg kun skal bruge et?