Matematik

20. september 2018 af kgsklo - Niveau: Universitet/Videregående

Hej alle
Nogen som kan hjælpe med den vedhæftede opgave

Tak på forhånd

Vedhæftet fil: IMG_3806.PNG

Brugbart svar (0)

Svar #1
20. september 2018 af swpply (Slettet)

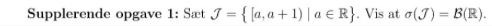
Lad $\mathcal{O}$ benævne familien af samtlige åbne mængder på $\mathbb{R}$ .

Følgende er et ufærdigt bevis for påstanden ovenfor, i den forstand at du selv må vise at (1) er sand.

Start med at vise $\sigma(\mathcal{J})\subseteq\mathcal{B(\mathbb{R})}$ . Eftersom $\mathcal{J}\subseteq\mathcal{O}$ har du at $\sigma(\mathcal{J})\subseteq\sigma(\mathcal{O})\equiv\mathcal{B}(\mathbb{R})$ .

Vi vil nu vise den modsatte inklusion $\sigma(\mathcal{J})\supseteq\mathcal{B(\mathbb{R})}$ . Begynd med bevise at

(1) $[a,\infty) = \bigcup_{n\in\mathbb{N}_0}[a+n,a+1+n)\in\sigma(\mathcal{J})$ .

Dermed gælder der at $\{[a,\infty)\mid a\in\mathbb{R}\}\subseteq\sigma(\mathcal{J})$ , hvorfor at $\mathcal{B}(\mathbb{R})\subseteq\sigma(\mathcal{J})$ eftersom at $\{[a,\infty)\mid a\in\mathbb{R}\}$ er et frembringer system for vores Borel $\sigma$ -algebra på $\mathbb{R}$ .

Vedhæftet fil:swpply.png

Brugbart svar (0)

Svar #2
21. september 2018 af swpply (Slettet)

Hov, undskyld det er da vist ikke helt rigtig hvad jeg har skrevet i #1. At $\mathcal{J}\subseteq\mathcal{O}$ er noget værre vås.

Et svar på opgave kunne istedet lyde:

Vedhæftet fil:swpply.png

Svar #3
21. september 2018 af kgsklo

Tusinde tak :-)

Skriv et svar til: Matematik

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.