Matematik

Hjælp til opgave om harmoniske svingninger

02. november 2018 af EMali - Niveau: A-niveau

Kan nogen hjælpe mig med denne opgave?

Vekselstrøm beskrives som en harmonisk svingning.
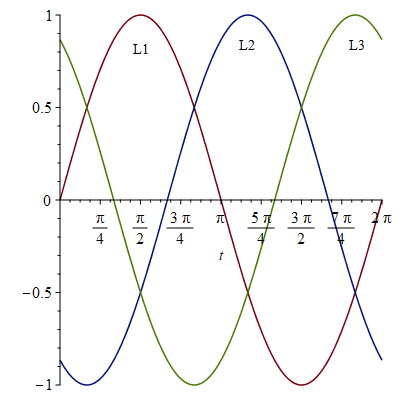
Trefaset vekselstrøm består af 3 ledere, hvor de harmoniske svingninger i lederne (ledningerne) er forskudt i forhold til hinanden som vist i filen.

Fasen L1 (rød) har forskriften L1(t)=sin(t)

- Find en forskrift for de 2 andre faser L2(t) og L3(t) og tegn de 3 kurver i samme koordinatsystem (det skal se ud som ovenfor, hvis det er rigtigt beregnet)

- Tegn L1(t)-L2(t). Hvor mange gange er amplituden større end for én fase?

Vedhæftet fil: Udklip.png

Brugbart svar (0)

Svar #1
02. november 2018 af mathon

Brugbart svar (0)

Svar #2
02. november 2018 af MatHFlærer

Brugbart svar (0)

Svar #3
02. november 2018 af mathon

$\small \small \begin{array}{rcl} L_1&=&\sin(t)\\ L_2&=&\sin\left (t-\tfrac{2\pi }{3} \right )\\ L_3&=&\sin\left (t-\tfrac{4\pi }{3} \right ) \end{array}$

Brugbart svar (0)

Svar #4
02. november 2018 af mathon

$\small L_1-L_2=\sqrt{3}\cdot \cos\left ( t-\tfrac{\pi }{3} \right )$
hvorfor
amplituden er: $\small \sqrt{3}$

Brugbart svar (0)

Svar #5
02. november 2018 af mathon

detaljer:

Generelt:
$\small a\cdot \cos(v)+b\cdot \sin(v)$

$\small a\cdot\left ( \cos(v)+\frac{b}{a}\cdot \sin(v) \right )$ $\small \textup{her s\ae ttes }\tan\left ( \beta \right )=\frac{\sin(\beta )}{\cos(\beta )}=\frac{b}{a}$

$\small a\cdot\left ( \cos(v)+\frac{\sin(\beta )}{\cos(\beta )}\cdot \sin(v) \right )$

$\small \frac{a}{\cos(\beta )}\cdot\left ( \cos(v)\cdot \cos(\beta )+\sin(\beta )\cdot \sin(v) \right )$

$\small \frac{a}{\cos(\beta )}\cdot \cos(v-\beta )$

$\small a\cdot \frac{1}{\cos(\beta )}\cdot \cos(v-\beta )$

$\small a\cdot \sqrt{1+\tan^2(\beta )}\cdot \cos(v-\beta )$

$\small a\cdot \sqrt{1+\frac{b^2}{a^2}}\cdot \cos(v-\beta )$

$\small \sqrt{a^2+b^2}\cdot \cos(v-\beta )$

...
som med

$\small \sin(t)-\sin\left ( t-\tfrac{2\pi }{3} \right )$

$\small \sin(t)-\left (\sin(t)\cdot\cos\left ( \tfrac{2\pi }{3} \right ) -\cos(t)\cdot \sin\left ( \tfrac{2\pi }{3} \right )\right )$

$\small \sin(t)-\left (-\sin(t)\cdot\cos\left ( \tfrac{\pi }{3} \right ) -\cos(t)\cdot \sin\left ( \tfrac{\pi }{3} \right )\right )$

$\small \sin(t)-\left (-\sin(t)\cdot\tfrac{1}{2} -\cos(t)\cdot \tfrac{\sqrt{3}}{2} \right )$

$\small \tfrac{\sqrt{3}}{2} \cdot \cos(t)+\tfrac{3}{2}\cdot \sin(t)$

$\small \sqrt{\left (\tfrac{\sqrt{3}}{2} \right )^2+\left ( \tfrac{3}{2} \right )^2}\cdot \cos(t-\tfrac{\pi }{3})\qquad \textup{da }\beta =\tan^{-1}\left ( \sqrt{3} \right )=\tfrac{\pi }{3}$

$\small \small \sqrt{3}\cdot \cos(t-\tfrac{\pi }{3})$

Skriv et svar til: Hjælp til opgave om harmoniske svingninger

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.