Matematik

Differentiere funktion via CAS

29. januar 2019 af WhatTheFu - Niveau: A-niveau

Hej alle!

Jeg sidder med opgaven her, hvor jeg er i gang med opgave a. Jeg har differentieret funktionen til $p*sin (t/2 +89) / 360)$ '

(π*sin(t/2 + 89)) / 360 og forsøger at solve på mit CAS værktøj for at finde f´(0) men får dette: t=2*(180 *n4-89) selvom jeg har skrevet t≤0t≤24

Hvordan skal jeg tolke det og regne videre med det?

Er der nogle der kan fortælle mig hvad det egentlig bliver til?

Og give nogle fif til løsning af de andre delopgaver?

Mange tak

Vedhæftet fil: opg 5.PNG

Brugbart svar (1)

Svar #1
29. januar 2019 af Larsdk4 (Slettet)

B) Sæt forskriften ind i wormat --> aflæs grafen --> svaret er max er 8 og mindst 6 i vanddybden

Brugbart svar (1)

Svar #2
29. januar 2019 af oppenede

a) Det der står inde i sinusen, dvs. (t-2)/2 løber længere end en 2pi ≈ 6.28 periode når t går fra 0 til 24, hvorfor sinus både antager sit maximum 1 og minimum -1 inden for 0 < t < 24. Forskriften afhænger lineært (og dermed monotont) af sinusen, hvilket betyder at funktionens maximum og minimum blot bestemmes ved at erstatte sin(...) med 1 og -1

Svar #3
30. januar 2019 af WhatTheFu

#2
a) Det der står inde i sinusen, dvs. (t-2)/2 løber længere end en 2pi ≈ 6.28 periode når t går fra 0 til 24, hvorfor sinus både antager sit maximum 1 og minimum -1 inden for 0 < t < 24. Forskriften afhænger lineært (og dermed monotont) af sinusen, hvilket betyder at funktionens maximum og minimum blot bestemmes ved at erstatte sin(...) med 1 og -1

Jeg har nu forsøgt med at indsætte 1 og -1, hvoraf det giver 0,000152 og -0,000152

Hvordan skal jeg bære mig af herfra, er tallene korrekte?

Brugbart svar (1)

Svar #4
30. januar 2019 af oppenede

Prøv at tegne og kigge på grafen for f i et koordinatsystem hvor t går fra 0 til 24

Brugbart svar (1)

Svar #5
10. februar 2019 af ringstedLC

#2: ... og addere med 7

#3: Hvis du har indsat intervallet "t≤0t≤24" ⇒ t ≤ 24, hvilket giver uendeligt mange løsninger.

Enten skrives: 0 ≤ t ∧ t ≤ 24 eller også skrives: 0 ≤ t ≤ 24.

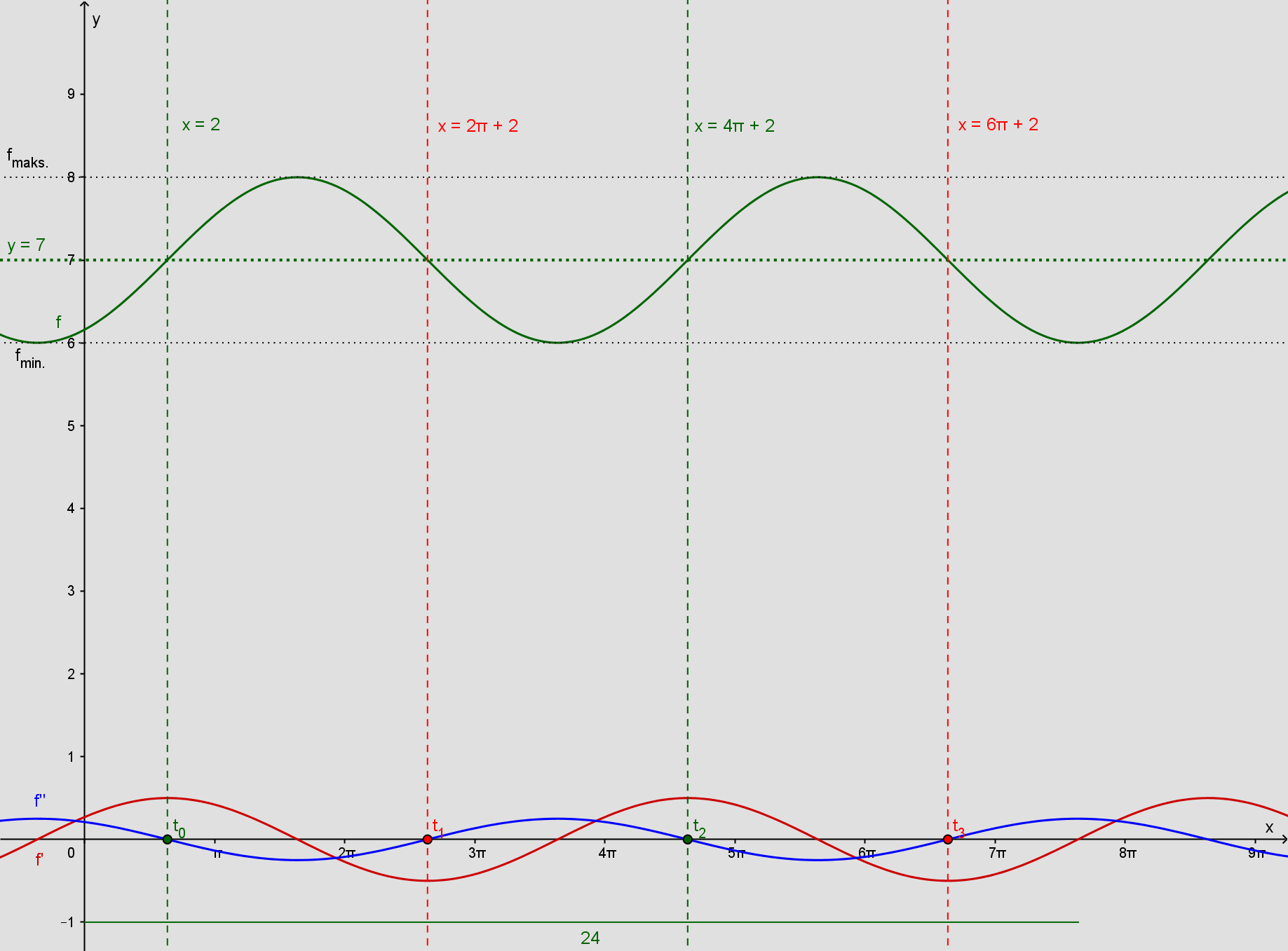
$\begin{align*} f_{ekstr.}(t)=7\pm1 \end{align*}$

b) Højvande er det første f_maks.(t)

$\begin{align*} f_{maks.}(t) &=7+1 \\ 8&=7+\sin\left ( \tfrac{t-2}{2} \right )\Updownarrow \\ 1&=\sin\left ( \tfrac{t-2}{2} \right )\Updownarrow \\ \tfrac{\pi}{2}&=\tfrac{t-2}{2}\Rightarrow t=\;?\Rightarrow Tidspunkt=12+t \end{align*}$

c) Næste højvande kommer én periode senere:

$\begin{align*} \sin\left ( \tfrac{t-2}{2} \right )=\sin\left ( \tfrac{t}{2}-\tfrac{2}{2} \right )&=\sin\left ( 0.5t-1 \right ) \\ Periode,\;\sin(ax-\varphi)&=\frac{2\pi}{a} \\ Periode_{\sin\left ( 0.5t-1 \right )}&=\;? \Rightarrow Tidspunkt=12+t_{b)}\;+\;? \end{align*}$

d) Vanddybden vokser hurtigst ved f'_maks.(t) som kan løses ved at sige f''(t) = 0, altså f'_ekstr.(t):

$\begin{align*} f(t) &= 7+\sin\left ( \frac{t-2}{2} \right )\;,\;0\leq t\leq24\Updownarrow \\ f(t) &= 7+\sin\left ( 0.5t-1 \right )\Updownarrow \\ f''(t) &= -0.25\cdot \sin(0.5t-1) \\ f''(t)=0 &= -0.25\cdot \sin(0.5t-1)\Updownarrow \\ 0 &= \sin(0.5t-1) \\ Generelt:0 &= \sin(x)\Rightarrow n\pi=x\;,\;n\in \mathbb{Z} \\ n\pi &= 0.5t-1\Updownarrow \\ t &= 2n\pi+2\Updownarrow \\ 0 &\leq 2n\pi+2\leq 24\Updownarrow \\ 0 &\leq n\leq 3\Rightarrow \left\{\begin{matrix} t=2\;,\;n=0\\ t=2\pi+2\;,\;n=1\\ t=4\pi+2\;,\;n=2 \\ t=6\pi+2\;,\;n=3 \\ \end{matrix}\right. \\ \end{align*}$

som giver størst ændring i vanddybden (De fire linjer på nedenstående figur).

Når vanddybden vokser hurtigst haves f'(t) > 0 ∧ f''(t) = 0 ⇒ f'_maks.(t) (De to grønne linjer):

$\begin{align*} f'(t)=0.5\cdot \cos\left(0.5t-1\right)>0\;\wedge f''(t)=0\;&,\;0\leq t\leq 24 \;,\;\left\{\begin{matrix}t_0=2 \\t_1=2\pi+2 \\t_2=4\pi+2 \\t_3=6\pi+2 \\\end{matrix}\right. \\ f'(t_0)=0.5\cdot \cos\left(0.5\cdot 2-1\right)=0.5>&\;0 \\ f'(t_1)=0.5\cdot \cos\left(0.5\cdot (2\pi+2)-1\right)=-0.5{\color{Red} \;<}&\;0 \\ f'(t_2)=0.5\cdot \cos\left(0.5\cdot (4\pi+2)-1\right)=0.5>&\;0 \\ f'(t_3)=0.5\cdot \cos\left(0.5\cdot (6\pi+2)-1\right)=-0.5{\color{Red} \;<}&\;0\Downarrow \\ f'(t)>0\;&\wedge f''(t)=0\Downarrow \\ Tidspunkt_1=12+t_0\;&,\;Tidspunkt_2=12+t_2 \end{align*}$

Vedhæftet fil:A_M_066 - Tidevand, sinus 2. afl. CAS_WhatTheFu.png

Skriv et svar til: Differentiere funktion via CAS

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.