Matematik

integraler ved substitution

12. februar 2019 af Teriperry - Niveau: B-niveau

det er den sidste opgave jeg ikke kan finde ud af, og forstår simpelthen ikke det med substitiution, så det ville være vildt fedt hvis jeg kunne få den forklaret og hjulpet med:

bestem følgende ubestemte integraler ved substitution

Vedhæftet fil: Skærmbillede 2019-02-12 kl. 19.07.27.png

Brugbart svar (0)

Svar #1
12. februar 2019 af peter lind

Svar #2
12. februar 2019 af Teriperry

#1

Brugbart svar (0)

Svar #3
12. februar 2019 af peter lind

a) substitutionen er t=x²+1 dt = 2xdx

b) t=x³-1 dt = 3x²dx

Generelt du skal se efter om en funktion indgår i kvadratrod, sin, logaritme eller lignende som her hvor det er kvrod(x²+1)

Brugbart svar (0)

Svar #4
12. februar 2019 af oppenede

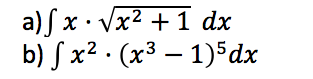
Substitution er det modsatte af kædereglen for differentation, som siger:
$\frac{d}{dx}f(g(x))=f'(g(x))g'(x)$
eller hvis man integrerer på begge sider:
$f(g(x))=\int f'(g(x))g'(x)dx$
hvilket er en mere passende måde at skrive det på ift. integration.

Hvis du i den første opgave ganger med 2 inde i integralet (og dividerer med 2 uden for), så står der:
$\frac{1}{2}\int2x\cdot\sqrt{x^2+1}\,dx$

Her kan man tydeligt se en indre funktion g(x)=x²+1, hvis afledede er faktor yderst i integranden.

Lad derfor
Og lad .

Dermed kan integranden skrives så det passer med kædereglen:
$\frac{1}{2}\int2x\cdot\sqrt{x^2+1}\,dx=\frac{1}{2}\int g'(x)f(g(x))\,dx = \frac{1}{2}f(g(x))$

Da så er

Dvs. den første giver

Brugbart svar (0)

Svar #5
13. februar 2019 af mathon

her sættes:
   $\small t=x^3-1\qquad\textup{og}\qquad\tfrac{1}{3}\mathrm{d}t=x^2\mathrm{d}x$
   hvoraf:
   $\small \int x^2\cdot \left ( x^3-1 \right )^5\mathrm{d}x=\int \left ( x^3-1 \right )^5 x^2\mathrm{d}x=\int t^5\cdot \tfrac{1}{3}\mathrm{d}t=\tfrac{1}{3}\int t^5\cdot \mathrm{d}t=$

$\small \tfrac{1}{3}\cdot \tfrac{1}{6}\cdot t^6+k=\tfrac{1}{18}\cdot t^6+k=\tfrac{1}{18}\cdot \left ( x^3-1 \right )^6+k$

Skriv et svar til: integraler ved substitution

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.