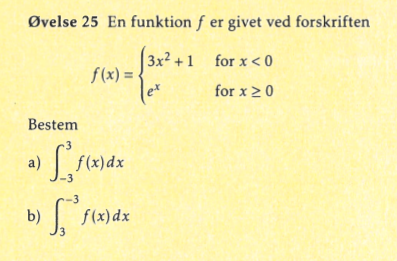Matematik

Integral opgave

21. marts 2019 af soso1111 - Niveau: B-niveau

Hej allesammen

Jeg har problemer med denne opgave kan jeg få lidt hjælp :)

Vedhæftet fil: lolo.PNG

Brugbart svar (0)

Svar #1
21. marts 2019 af peter lind

Brugbart svar (0)

Svar #2
21. marts 2019 af ringstedLC

$\begin{align*} \int_{-3}^{3}f(x)\;dx &= \int_{-3}^{0}3x^2+1\;dx +\int_{0}^{3}e^x\;dx \end{align*}$

Brugbart svar (1)

Svar #3
21. marts 2019 af peter lind

Brug indskudssætningen ∫_-3³f(x)dx= ∫_-3⁰f(x)dx+∫₀³f(x)dx

Svar #4
21. marts 2019 af soso1111

#2 og #3 kan jeg få mere hjælp, jeg har prøvet at lave den men jeg er meget sikker på at det er forkert

Brugbart svar (0)

Svar #5
21. marts 2019 af peter lind

Hvad har du fået ?

Svar #6
21. marts 2019 af soso1111

# 5

((e^3)-1)/ln(e)+39, forresten måtte man i selve opgaven ikke bruge cas værktøjer eller lommeregner, men altså brugt lommeregner da jeg ikke kunne komme videre.

Brugbart svar (0)

Svar #7
21. marts 2019 af ringstedLC

$\begin{align*} \int_{-3}^{3}f(x)dx &= \int_{-3}^{0}3x^2+1dx+\int_{0}^{3}e^xdx \\ &= \begin{bmatrix}x^3+x\end{bmatrix}\begin{smallmatrix} 0\\-3\end{smallmatrix}+\begin{bmatrix}e^x\end{bmatrix}\begin{smallmatrix} 3\\0\end{smallmatrix} \\ &= 0-\left ( (-3)^3+(-3) \right )+e^3-e^0 \\ &= 30+e^3-1=29+e^3=49.09 \\ \end{align*}$

$\begin{align*} \int_{3}^{-3}f(x)dx &= \int_{0}^{-3}3x^2+1dx+\int_{3}^{0}e^xdx \\ &= \begin{bmatrix}x^3+x\end{bmatrix}\begin{smallmatrix} -3\\0\end{smallmatrix} +\begin{bmatrix}e^x\end{bmatrix}\begin{smallmatrix} 0\\3\end{smallmatrix} \\ &= \left ( (-3)^3+(-3) \right )+e^0-e^3 \\ &= -30+1-e^3=-29-e^3=-49.09 \end{align*}$

Brugbart svar (0)

Svar #8
21. marts 2019 af peter lind

det er forkert. En stamfunktion til 3x²+1 er x³+x og en stamfunktion til e^x er e^x

Skriv et svar til: Integral opgave

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.