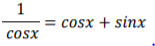Matematik

Cos og sin ligning

11. april 2019 af Ryder - Niveau: B-niveau

Hej jeg er igang med en aflevering og skal løse den her ligning. Har prøvet diverse metoder men synes ikke at det virker rigtigt. Er der måske nogle derude der kunne forklare hvordan man kunne gribe den an?

Tak på forhånd

- Ryder

Vedhæftet fil: Udklip.PNG

Brugbart svar (0)

Svar #1
11. april 2019 af mathon

Brugbart svar (0)

Svar #2
11. april 2019 af peter lind

Brugbart svar (0)

Svar #3
11. april 2019 af peter lind

Gang ligningen med cos(x)

Brug idiotformlen på cos2(x)

Træk 1 over på vensre side

Du har nu en 2.gradsligning i sin(x). Løs denne.

Svar #4
11. april 2019 af Ryder

#3
Gang ligningen med cos(x)

Brug idiotformlen på cos2(x)

Træk 1 over på vensre side

Du har nu en 2.gradsligning i sin(x). Løs denne.

Idiotformlen?

Brugbart svar (0)

Svar #5
11. april 2019 af mathon

$\small \tfrac{1}{\cos(x)}=\cos(x)+\sin(x)\qquad x\neq \tfrac{\pi}{2}+p\cdot\pi\qquad p\in\mathbb{Z}$

Brugbart svar (0)

Svar #6
11. april 2019 af peter lind

#4 cos²(x)+sin²(x) = 1

Svar #7
11. april 2019 af Ryder

#6
#4 cos²(x)+sin²(x) = 1

Men hvad sker der når man gang cos(x) med sin(x) ?

Brugbart svar (0)

Svar #8
11. april 2019 af oppenede

Jeg kan ikke se meningen med det #3 siger...

Jeg ville dividere med cos(x) i alle led, og bruge sin(x)/cos(x) = tan(x)

$\frac{1}{\cos^2(x)}=\tan(x)+1$

Desuden er 1/cos²(x) = sec²(x) = 1 + tan²(x)

$1+\tan^2(x)=\tan(x)+1$

Som er en andengradsligning mht tan(x).

For at indse 1/cos²(x) = 1 + tan²(x), så tænk på højresiden som den kvadrerede hypotinuse i den trekant i enhedscirklen hvor radius og tangens er kateter. Der er også en trekant i enhedscirklen med sinus og cosinus som kateter og hypotinuse 1. Skalafaktoren fra denne til førnævnte er 1/cos(x), og da det er den kvadredede hypotinuse som beregnes skal 1 skalleres med 1/cos²(x) for at blive til 1 + tan²(x).

Svar #9
11. april 2019 af Ryder

#8
Jeg kan ikke se meningen med det #3 siger...

Jeg ville dividere med cos(x) i alle led, og bruge sin(x)/cos(x) = tan(x)

$\frac{1}{\cos^2(x)}=\tan(x)+1$

Desuden er 1/cos²(x) = sec²(x) = 1 + tan²(x)

$1+\tan^2(x)=\tan(x)+1$

Som er en andengradsligning mht tan(x).

For at indse 1/cos²(x) = 1 + tan²(x), så tænk på højresiden som den kvadrerede hypotinuse i den trekant i enhedscirklen hvor radius og tangens er kateter. Der er også en trekant i enhedscirklen med sinus og cosinus som kateter og hypotinuse 1. Skalafaktoren fra denne til førnævnte er 1/cos(x), og da det er den kvadredede hypotinuse som beregnes skal 1 skalleres med 1/cos²(x) for at blive til 1 + tan²(x).

Sorry jeg er stadig lidt forvirret omkring det hele

Brugbart svar (0)

Svar #10
12. april 2019 af mathon

$\small \tfrac{1}{\cos(x)}=\cos(x)+\sin(x)\qquad x\neq \tfrac{\pi}{2}+p\cdot\pi\qquad p\in\mathbb{Z}$

$\small 1=\cos^2(x)+\cos(x)\cdot \sin(x)$

$\small 1=1-\sin^2(x)+\cos(x)\cdot \sin(x)$

$\small 0=-\sin^2(x)+\cos(x)\cdot \sin(x)$

$\small \sin^2(x)-\cos(x)\cdot \sin(x)=0$

$\small \sin(x)\cdot \left (\sin(x)-\cos(x) \right )=0$

$\small x=\left\{\begin{array}{ll} p\cdot \pi \\&p\in\mathbb{Z}\\ \frac{\pi }{4}+p\cdot \pi \end{array}\right.$

Svar #11
13. april 2019 af Ryder

#10
$\small \tfrac{1}{\cos(x)}=\cos(x)+\sin(x)\qquad x\neq \tfrac{\pi}{2}+p\cdot\pi\qquad p\in\mathbb{Z}$

$\small 1=\cos^2(x)+\cos(x)\cdot \sin(x)$

$\small 1=1-\sin^2(x)+\cos(x)\cdot \sin(x)$

$\small 0=-\sin^2(x)+\cos(x)\cdot \sin(x)$

$\small \sin^2(x)-\cos(x)\cdot \sin(x)=0$

$\small \sin(x)\cdot \left (\sin(x)-\cos(x) \right )=0$

$\small x=\left\{\begin{array}{ll} p\cdot \pi \\&p\in\mathbb{Z}\\ \frac{\pi }{4}+p\cdot \pi \end{array}\right.$

Hvor kommer cos^2x fra?

Skriv et svar til: Cos og sin ligning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.